Challenge 9 ("10000")

Description

Ok hotshot, this is it, the only thing standing between you and slightly less internet anonymity.

Writeup

Phew. This was one hell of a ride.

The download for this challenge is a 963 MB (?!) 7-zip file, containing a single EXE that decompresses to a whopping 1.07 GB. Along with the somewhat ominous name "10000", this sends a slightly spooky message that some craziness may lurk inside.

As part of my routine PE file triage, I opened up the file in Resource Hacker. I seemed to have stumbled upon the reason for the name of the challenge, as it contains exactly 10000 resources.

Funnily enough, Resource Hacker doesn't seem to have accounted for such a number of resources, as selecting e.g. the last one in the GUI pops up a message box with the assertion that an integer overflow has occurred. (I did not investigate this further, though I may look for an alternative resource editor for my future endeavours.)

It appeared similarly strange that each of the resources (or those I cared to look at anyways) kind of resembled a PE file at first glance, though disturbed somehow. You can make out the general structure of a Portable Executable — the DOS stub, PE header and names of sections, but seemingly interweaved with random bytes.

Keeping this in the back of our minds, let's quickly glance at the executable code.

The entry point is structured like a normal C++ executable, so we can navigate to the main function at preferred virtual address (PVA) 0x140001E87. Fortunately, this time there are no crazy obfuscations hindering the decompiler from working well (yet), so we can get a good basic idea about what the program does. The below pseudo-code is a simplified representation thereof, with my variable and function names and comments.

#include <fstream>
#include <iostream>
#include <memory>
#include <vector>

static std::vector<std::unique_ptr<LoadedDll>> g_loaded_dlls;
static uint32_t g_dll_sums[10000];

static const uint32_t g_dll_sums_reference[10000] = { /* ... */ };
static const uint8_t  g_flag_ciphertext[80]       = { /* ... */ };
static const uint8_t  g_aes_iv[16]                = { /* ... */ };

struct LoadedDll;

int main(int argc, const char **argv, const char **envp)
{
    std::cout << "checking license file..." << std::endl;

    std::ifstream ifstream_license("license.bin", std::ios::binary);
    size_t license_filesize = filesize(ifstream_license);

    if (license_filesize != 340000)
        return (std::cout << "invalid license file" << std::endl), 1;

    ifstream_license.seekg(0, std::ios_base::beg); // probably, did not check...

    auto license_buf = std::unique_ptr<uint8_t[](license_filesize);
    ifstream_license.read(license_buf.get(), license_filesize);

    auto license_hash = std::array<uint8_t, 32>();
    sha256(license_buf.get(), license_buf.get() + license_filesize, license_hash.begin(), license_hash.end());

    auto used_dlls = std::vector<bool>(10000, false);

    uint8_t *lic_iter = license_buf.get();

    for (int i = 0; i < 10000; ++i)
    {
        // The first 2 bytes of every license chunk give a resource ID.
        uint16_t resource_num = *(uint16_t *)lic_iter;
        if (resource_num >= 10000)
            return (std::cout << "invalid license file" << std::endl), 1;

        // Cannot use the same resource twice.
        if (used_dlls[resource_num] == true)
            return (std::cout << "invalid license file" << std::endl), 1;
        used_dlls[resource_num] = true;

        // Advance the iterator.
        lic_iter += sizeof resource_num;

        LoadedDll *loaded_dll = load_dll_from_resource(resource_num); // Writes to g_loaded_dlls as a side effect.

        bool (*check)(uint8_t *) = (bool (*)(uint8_t *))get_proc_address(
            loaded_dll->exports,
            std::string("_Z5checkPh")
        );

        // Call an exported function from the resource DLL, must return 1.
        if (!check(lic_iter))
            return (std::cout << "invalid license file" << std::endl), 1;

        // Advance the iterator -- the 'checked' chunk likely has 32 bytes.
        lic_iter += 32;

        update_dllsums_and_unload_all(i); // Reads and writes g_dll_sums as a side effect.
    }

    if (0 != memcmp(g_dll_sums, g_dll_sums_reference, sizeof g_dll_sums))
        return (std::cout << "invalid license file" << std::endl), 1;

    std::cout << "license valid!" << std::endl;

    char flag[80] = { 0 };

    decrypt_aes_cbc(
        g_flag_ciphertext,
        80,
        license_hash.data(), // AES key
        license_hash.size(), // AES key size (32)
        &g_aes_iv,           // CBC initialization vector (constant)
        flag.data(),
        flag.size()
    );

    std::cout << flag_plaintext << std::endl;
}

Of course, the initial decompiled code in IDA was far from the one listed above, but reverse-engineering it was not particularly hard compared to the rest of the challenge. Naturally, I should also clarify what the load_dll_from_resource and update_dllsums_and_unload_all functions do, and how.

In the former case, the semantics are fairly self-explanatory, but the loading mechanism is worth a closer description, especially since we saw earlier that the resources are not valid PE files in their raw form. Illustrated in my high-level C++ model below, the binary implements its own minimal version of a Windows loader, loading DLLs into RWX memory regions, resolving and binding imports, and applying relocations. One key difference between this logic and standard DLL loading is that imported DLLs whose names start with 4 decimal digits are loaded from the EXE resources, not from the standard DLL search path using LoadLibrary.

#include <algorithm>
#include <cstdlib>
#include <windows.h>
#include <winnt.h>

struct LoadedDll
{
    uint16_t num;       // 0x0
    void    *ptr_image; // 0x8
    uint64_t exports;   // 0x10
    uint64_t field_18;  // 0x18
    uint64_t field_20;  // 0x20
    uint64_t field_28;  // 0x28
    uint64_t field_30;  // 0x30
    uint64_t field_38;  // 0x38

    ~LoadedDll()
    {
        VirtualFree(ptr_image, 0, MEM_RELEASE);
    }
}

LoadedDll *load_dll_from_resource(uint16_t id)
{
    auto found = std::find_if(
        g_loaded_dlls.begin(),
        g_loaded_dlls.end(),
        [](const auto &dll) { return dll->num == id; }
    );

    if (found != g_loaded_dlls.end())
        return found->get();

    auto dll = std::make_unique<LoadedDll>();
    dll.num = id;

    HRSRC   res_info = FindResourceA(NULL, MAKEINTRESOURCE(id), RT_RCDATA);
    HGLOBAL res_data = LoadResourceA(NULL, res_info);
    LPVOID  res_buf  = LockResource(res_data)
    DWORD   res_size = SizeOfResource(NULL, res_info);

    // Custom (?) decompression routine -- only computes inflated size.
    uint32_t decompressed_size = get_decompressed_size(res_buf, res_size, 0);

    auto decompressed_data = std::vector<uint8_t>(decompressed_size);
    auto decompressed_buf = decompressed_data.data();

    // Custom (?) decompression routine.
    decompress_buffer(res_buf, decompressed_buf, res_size, decompressed_size, 0);

    auto ptr_pe_header = std::reinterpret_cast<PIMAGE_NT_HEADERS64>(
        (decompressed_buf + *(uint32_t *)(decompressed_buf + 0x3C))
    );

    LPVOID dll_image = VirtualAlloc(
        NULL,
        ptr_pe_header->OptionalHeader.SizeOfImage,
        MEM_COMMIT | MEM_RESERVE,
        PAGE_EXECUTE_READWRITE
    );
    dll.ptr_image = dll_image;

    auto ptr_section_header = std::reinterpret_cast<PIMAGE_SECTION_HEADER>(
        (char *)ptr_pe_header->OptionalHeader + ptr_pe_header->FileHeader.SizeOfOptionalHeader
    );

    for (int i = 0; i < ptr_pe_header->FileHeader.NumberOfSections; ++i)
    {
        memcpy(
            (char *)dll_image + ptr_section_header->VirtualAddress,
            &decompressed_buf[ptr_section_header->PointerToRawData],
            ptr_section_header->SizeOfRawData
        );
        ++ptr_section_header;
    }

    auto first_import_descriptor = std::reinterpret_cast<PIMAGE_IMPORT_DESCRIPTOR>(
        (char *)dll_image + ptr_pe_header->OptionalHeader.DataDirectory[1].VirtualAddress;
    );

    for (
        PIMAGE_IMPORT_DESCRIPTOR import_descriptor = first_import_descriptor;
        import_descriptor->Name != 0;
        ++import_descriptor
    ) {
        char *dll_name = (char *)dll_image + import_table->Name;
        auto import_thunk = std::reinterpret_cast<QWORD *>(
            (char *)dll_image + import_descriptor->FirstThunk
        );

        // If the first four bytes of the DLL name are not all digits (or below), it's a standard import.
        if (dll_name[0] - '0' > 9 || dll_name[1] - '0' > 9 || dll_name[2] - '0' > 9 || dll_name[3] - '0' > 9)
        {
            HMODULE lib = LoadLibraryA(dll_name);
            while (*import_thunk)
            {
                char *import_name = (char *)dll_image + *import_thunk;
                auto import_addr = std::static_cast<QWORD>(GetProcAddr(lib, import_name + 2));
                *import_thunk++ = import_addr;
            }
        }
        // Otherwise, the DLL comes from the resources.
        else
        {
            uint16_t import_id = atoi(dll_name);
            LoadedDll *import_dll = load_dll_from_resource(import_id);

            while (*import_thunk)
            {
                char *import_name = (char *)dll_image + *import_thunk;
                auto import_addr = get_proc_address(&import_dll->exports, std::string(import_name + 2));
                *import_thunk++ = import_addr;
            }
        }
    }

    // Parse export directory of loaded DLL.
    auto export_directory = std::reinterpret_cast<PIMAGE_EXPORT_DIRECTORY>(
        (char *)dll_image + ptr_pe_header->OptionalHeader.DataDirectory[0].VirtualAddress;
    );
    for (int i = 0; i < export_directory->NumberOfNames; ++i)
    {
        // ...
    }

    // Parse relocation directory of loaded DLL.
    auto first_relocation_entry = std::reinterpret_cast<PIMAGE_BASE_RELOCATION>(
        (char *)dll_image + ptr_pe_header->OptionalHeader.DataDirectory[5].VirtualAddress;
    );
    for (/* ... */)
    {
        // Apply relocations...
    }

    auto dll_entry_point = std::reinterpret_cast<BOOL (*)(uint32_t *, DWORD, LPVOID)>(
        (char *)dll_image + ptr_pe_header->OptionalHeader.AddressOfEntryPoint
    );

    dll_entry_point(&g_dll_sums, DLL_PROCESS_ATTACH, NULL);

    g_loaded_dlls.push_back(std::move(dll));
    return g_loaded_dlls[g_loaded_dlls.size() - 1].get();
}

Note: By the way, if you didn't know, all of the definitions for "winnt.h" structures (like IMAGE_NT_HEADERS and similar) and pointers (P...) are by default available in IDA and can make the decompiled code much clearer; I highly recommend taking advantage of them.

An important piece of the puzzle are the functions I named get_decompressed_size (0x140002690) and decompress_buffer (0x1400035E8). For a person like me, who has no background in compression algorithms, these functions are rather hard to follow. This is one of the cases where I copied the code, wrapped it in some context, and let a large language model (LLM) do the pattern matching. This is a good task for an LLM, since it involves reading a sequence of tokens in some language (pseudo-C), understanding the relationships between these tokens, and translating the "message" into a different kind of language (a human-readable high-level summary) — precisely the kind of activity transformers were designed and trained to do. The second reason why it is a suitable task for an LLM is that the claims made by the model are easily verifiable.

My LLM of choice gave the following answer:

This function is a custom LZ-type decompression routine — most likely an LZSS/LZ77 variant with bitstream-based control and sliding-window backreferences.

This made it clear to me what the subroutines were for, as the model's conclusion fit well into the context of the surrounding code and my mental model of the program. I followed up with more details about how the buffers being decompressed appear to be corrupted PE files (and included a hexdump snippet), to which the model reponded in an affirmative way.

In short: the challenge likely stores “disturbed” or compressed PE files, and sub_1400035E8 is the routine that decompresses them back into valid PE images in memory.

At this point, I suspected that it may be needed or beneficial to extract and decompress the resources myself. Later, I confirmed this to be the case and decided to dump all DLLs to disk. Based on one instance, I knew that a 118 KB byte resource decompressed to a 380 KB DLL, meaning the sum of the sizes of all extracted DLLs would be about 4 GB. This seemed acceptable, so I wrote a simple C++ program to do the job.

Decompressing and dumping the DLLs

One way to decompress the resources would be to reimplement the algorithm from scratch based on the decompiled functions. A much simpler (or lazier) way, which I decided to utilize, is to dump the function machine code and include it in my program directly. This was possible because both decompression routines only contained arithmetic instructions on the input/output buffer and stack memory accesses, and did not call any subroutines or reference global variables. Hence, as long as I could match the calling ABI, there would be no issue.

I included the dumped function bytes in a header called inflate.hpp,

#pragma once
#pragma section("extcode",read,execute)

#include <cstdint>

using get_decompressed_size_t = int64_t (*)(uint8_t *buf, int64_t size, int eq_0);
using decompress_buffer_t = void (*)(uint8_t *src, uint8_t *dst, int64_t src_size, int64_t dst_size, int64_t offset);

__declspec(allocate("extcode"))
unsigned char get_decompressed_size[] = { /* ... */ };

__declspec(allocate("extcode"))
unsigned char decompress_buffer[] = { /* ... */ };

and called them from my inflate_dll.cpp.

#include <cstdio>
#include <cstdint>
#include <string>
#include <windows.h>

#include "inflate.hpp"

int write_dll_file(unsigned long id, uint8_t *buf, int64_t size)
{
    char filename[256];
    if (-1 == sprintf_s(filename, sizeof filename, "%04lu.dll", id))
        return fprintf(stderr, "Error sprintf_s\n"), 1;

    FILE *outf = fopen(filename, "wb");
    if (!outf)
        return fprintf(stderr, "Error fopen\n"), 1;

    if (size != fwrite(buf, sizeof *buf, size, outf))
        return fprintf(stderr, "Error fwrite\n"), 1;

    fclose(outf);
    return 0;
}

int main(int argc, char **argv)
{
    if (argc != 2)
        return fprintf(stderr, "Usage: inflate_dll.exe <index>\n"), 1;

    std::string rsrc_s(argv[1]);
    unsigned long rsrc_idx = std::stoul(rsrc_s);

    HMODULE hExe = LoadLibraryA("10000.exe");
    if (!hExe)
        return fprintf(stderr, "LoadLibraryA failed. Make sure 10000.exe is in the current dir.\n");

    HRSRC hResInfo = FindResourceA(hExe, MAKEINTRESOURCE(rsrc_idx), RT_RCDATA);
    if (!hResInfo)
        return fprintf(stderr, "FindResourceA failed. GL...\n");

    HGLOBAL hResData = LoadResource(hExe, hResInfo);
    LPVOID  res_buf  = LockResource(hResData);
    DWORD   res_size = SizeofResource(hExe, hResInfo);

    int64_t inflated_size = ((get_decompressed_size_t)&get_decompressed_size)((uint8_t*)res_buf, res_size, 0);
    printf("Inflated size: %lld\n", inflated_size);

    uint8_t *inflated_buf = new uint8_t[inflated_size];
    ((decompress_buffer_t)&decompress_buffer)((uint8_t*)res_buf, inflated_buf, res_size, inflated_size, 0);

    return write_dll_file(rsrc_idx, inflated_buf, inflated_size);
}

(Yes, inflated_buf is leaked, no, it doesn't matter.)

I ran this program in a loop for every i from 0 to 9999, and sure enough, I was greeted with 10000 DLLs in my working directory.

Understanding the license validation logic

As I promised earlier, I will now touch on the update_dllsums_and_unload_all function (VA 0x140001D9F). Since it mutates g_dll_sums, the array that is later checked against a read-only reference, it's clearly highly relevant. Fortunately, it's also very simple:

void record_loaded_counts_and_unload_all(int iteration_i)
{
    for (auto dll = g_loaded_dlls.begin(); dll != g_loaded_dlls.end(); ++dll)
        g_dll_sums[dll->num] += iteration_i;
    g_dll_sums.clear(); // Destructors call VirtualFree.
}

Simply put, after each iteration i, this code increments the counters (or rather sums) for all DLLs loaded (directly or transitively) in this iteration by i. (Remember that load_dll_from_resource calls itself recursively until all transitive imports are loaded.)

This likely means that g_dll_sums_reference tells us what these sums should equal for each DLL after all 10000 iterations are finished. However, before jumping to such conclusions, we should look at the other place where g_dll_sums_reference could possibly be mutated, which is when it is passed to the DllMain of loaded DLLs, in place of the usual module handle.

Understanding the DLL check functions

Just to recap: The program accepts a 340,000 byte license file consisting of 10,000 blocks of a resource index (2 bytes) and some block of data (32 bytes). In order for the license to be accepted as valid, each DLL resource must be directly loaded exactly once, and the sum of iteration indexes in which a particular DLL was loaded transitively must match a given hard-coded value (for each resource individually). Furthermore, the bool check(uint8_t*) function exported by each DLL must return 1 (true) for the 32 byte buffer passed to it.

Based on some quick glances, the DLLs share the same general structure. It is therefore likely worth analyzing one in depth and generalizing afterwards. I randomly picked 0000.dll for analysis.

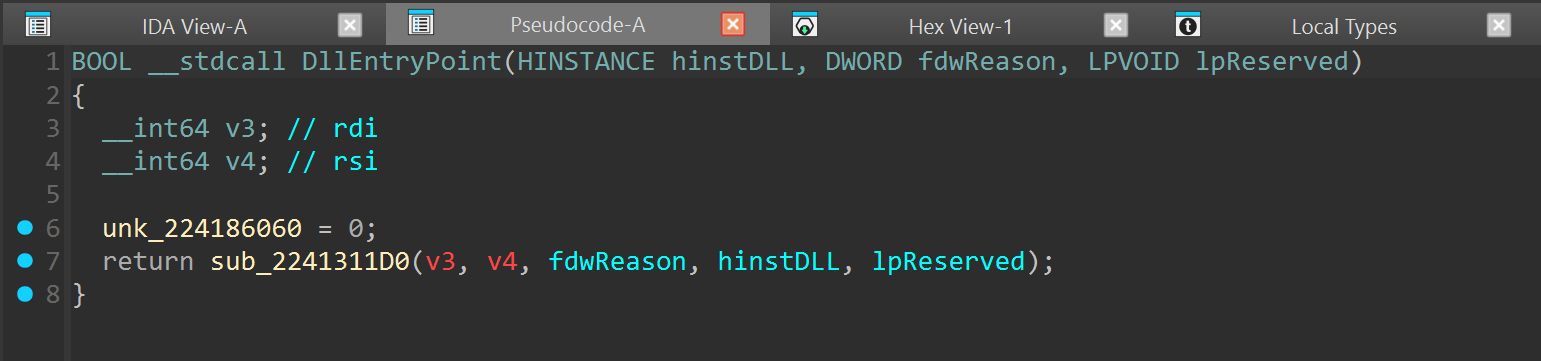
For some bizzare, to me unknown reason, IDA Pro struggles to analyze the DLL code. My best guess is that it identifies the compiler as GCC and assumes the System-V calling convention, in any case, I have not found a way to convince IDA to use the standard Windows 64-bit calling convention by default, without retyping all functions one by one.

Eventually, I found it the least painful to use Binary Ninja (free version) for high-level code browsing and data flow inspection and IDA Pro for decompiling specific functions (after typing them correcly), as Binary Ninja may not have struggled with Windows calling conventions, but it did struggle a lot with 128-bit integer types and arithmetic instructions (such as the completely unimplemented sbb or Integer Subtraction With Borrow).

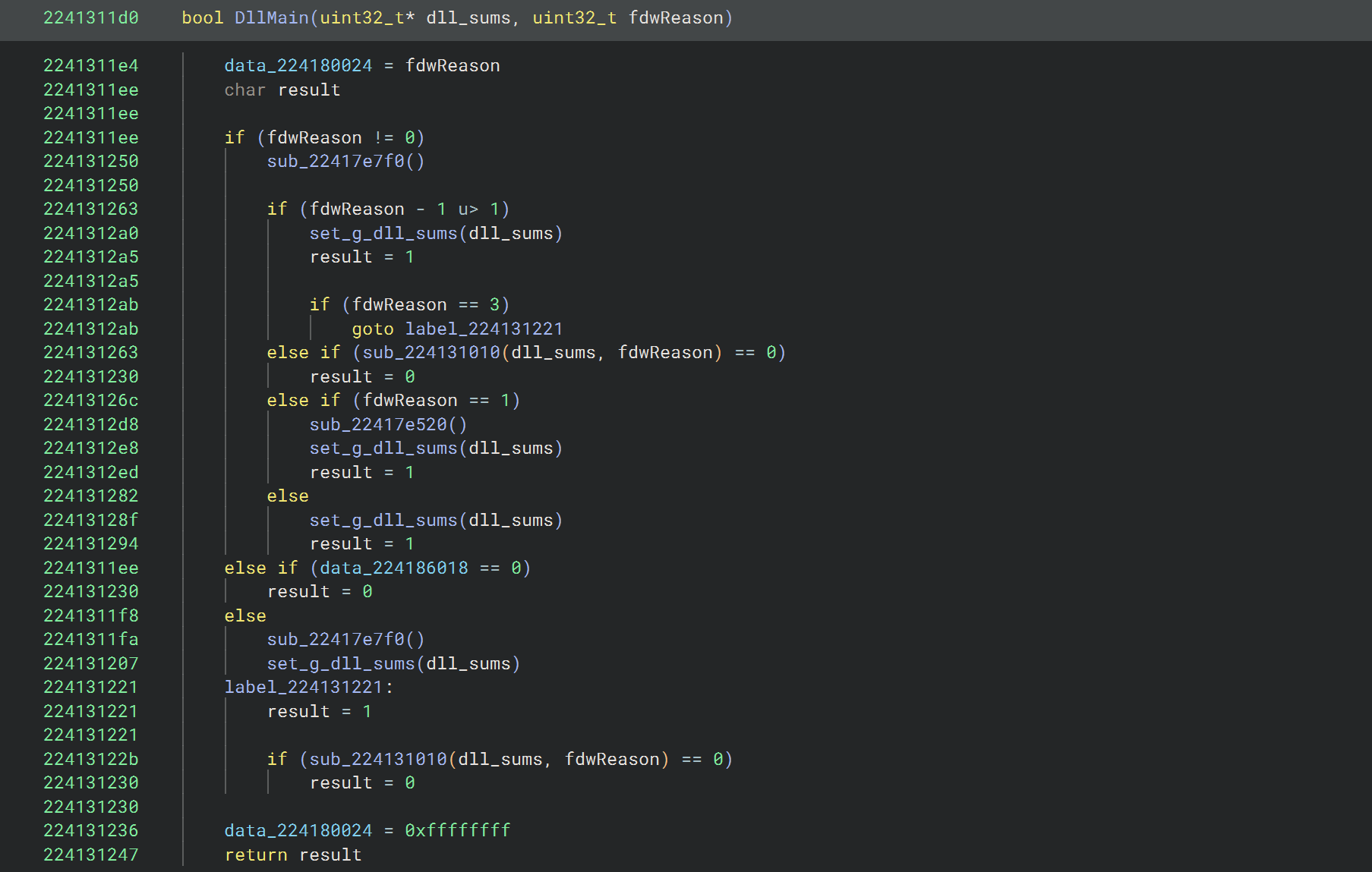
Analyzing the DllMain-like function with Binary Ninja revealed that pretty much the only thing done that is unrelated to the MSVC runtime is to save the pointer to the g_dll_sums array (passed to the DLL entry point in place of the module handle) to a global variable.

With the entry point out of the way, let's look at the check function.

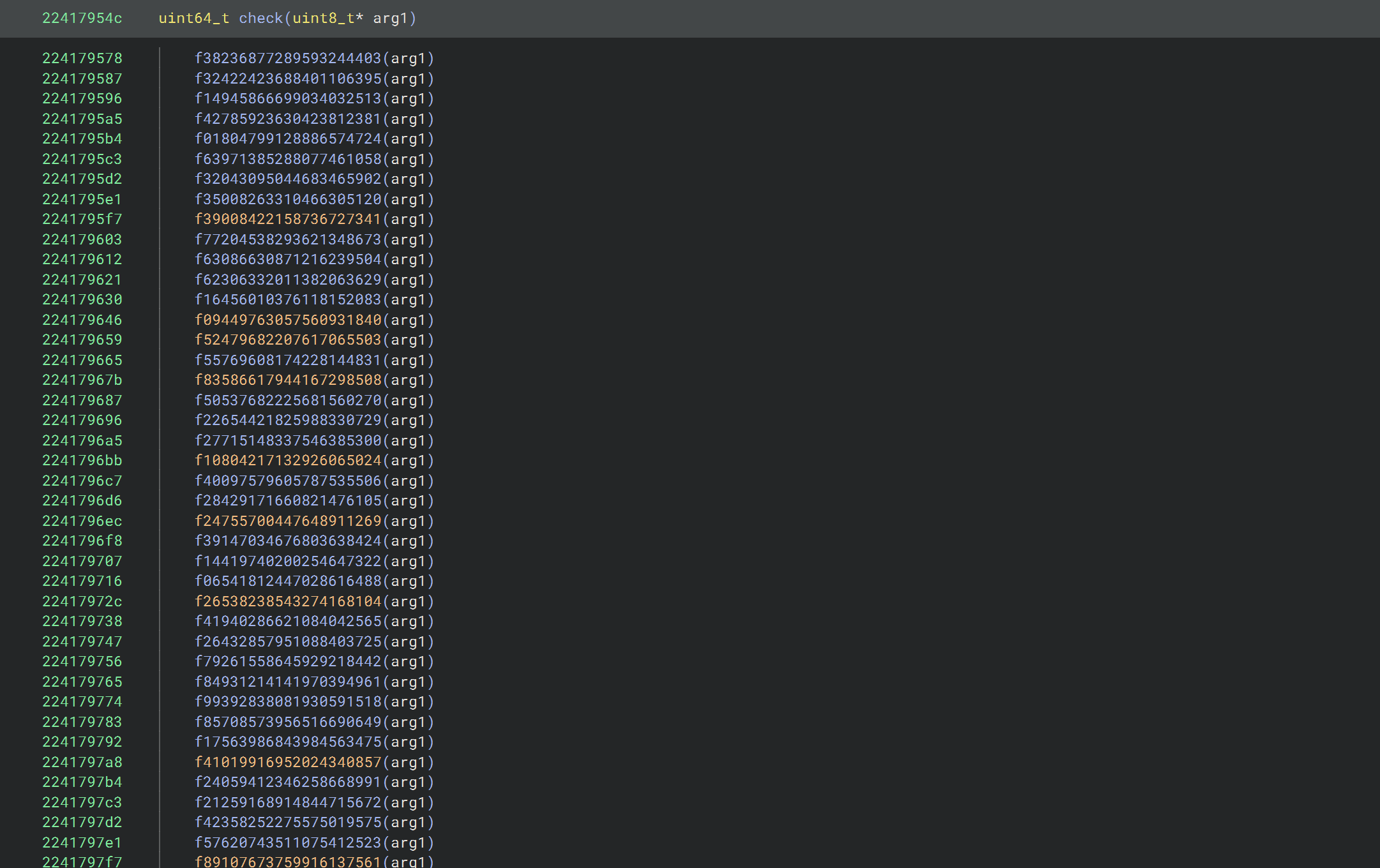
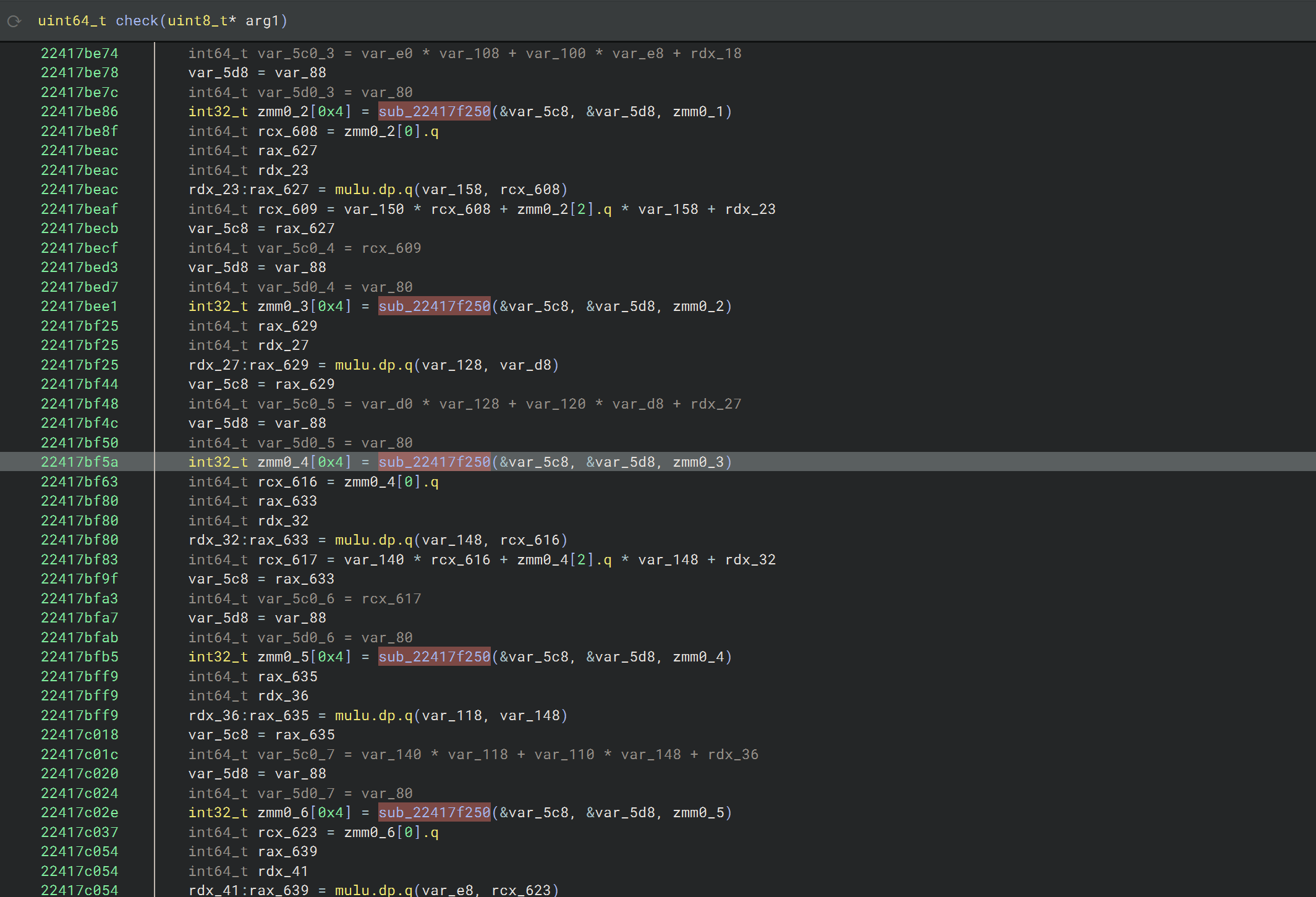
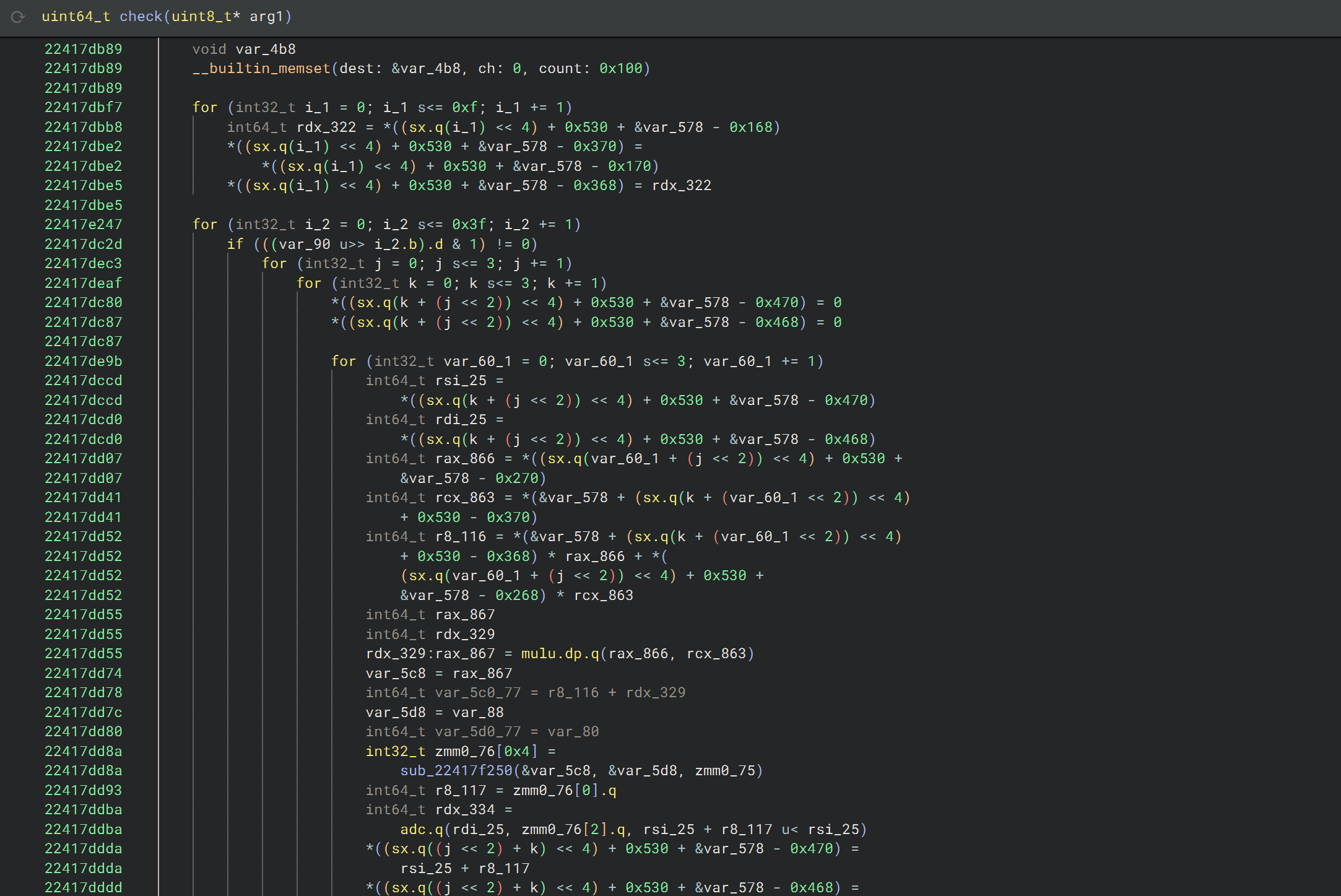
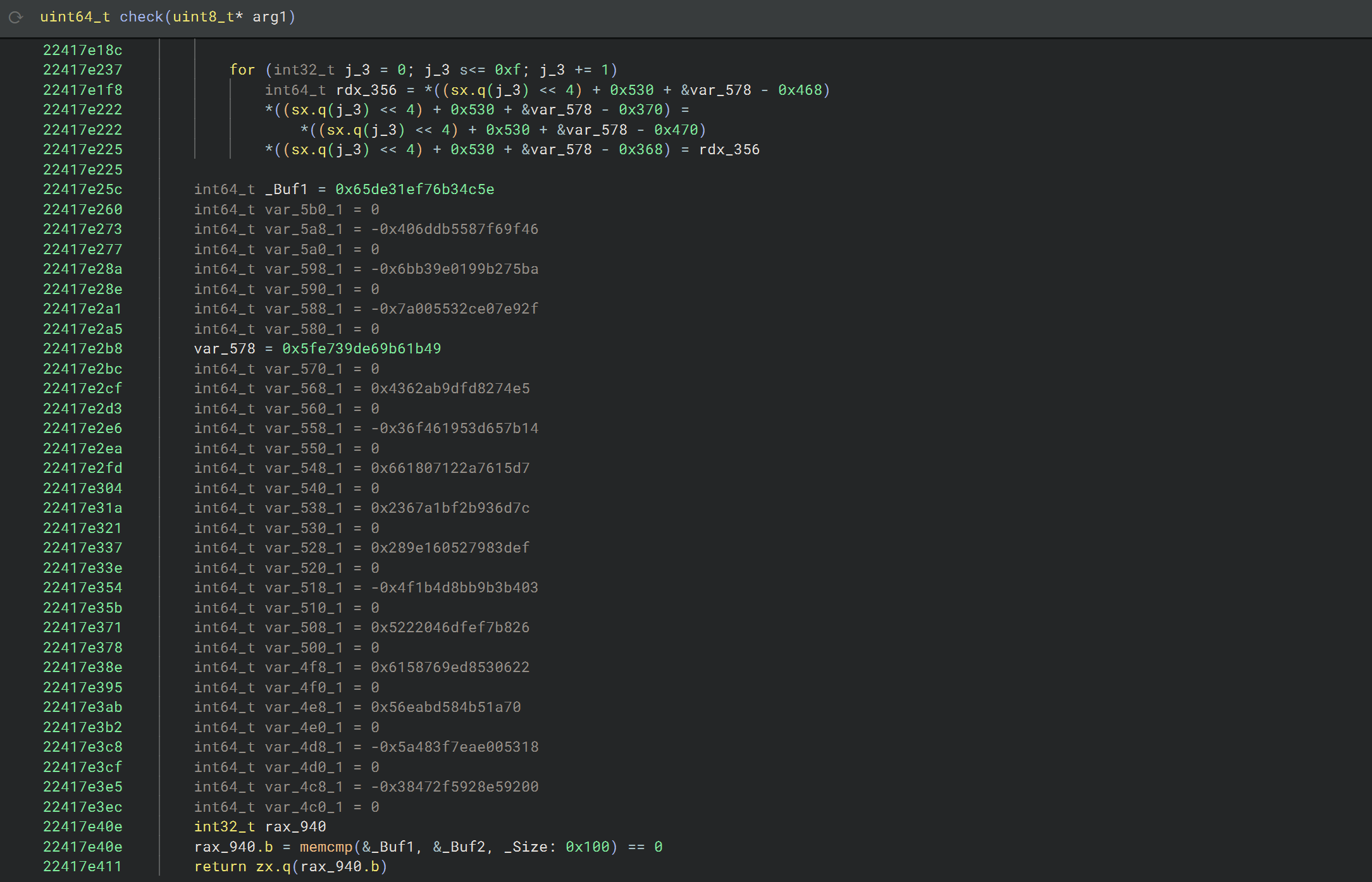
As you can probably tell, the check function looks huge. In the four screenshots above, you can see that first, at the very start, a large number of functions (some native to the DLL, some imported from other DLLs) are called in succession, operating only on the input buffer (likely modifying it in-place). Next, some arithmetic is done along with repeated calls to another function, with the second argument often being the same. Then, there is a part with multiple nested loops, with occasional calls to that same function, and finally, you can see the return value being computed by comparing two buffers for equality.

Let's start with the sequence of f* functions called at the beginning. As you inspect some of them, you will eventually notice that each function is one of three types, with seemingly only the hardcoded constants being randomized across all of them.

The first is a whitened substitution:

// Substitution
void f41552919119109981224(uint8_t* arg1)
{
    *(uint32_t*)arg1 ^= g_dll_sums[/* ID of the DLL this function is from */];

    BYTE sbox[256] = { ... constant ... };

    for (int i = 0; i < 32; i += 1)
        arg1[i] = sbox[arg1[i]];
}

The second a whitened permutation:

// Permutation
void f97389622909912273755(uint8_t* arg1)
{
    *(uint32_t*)arg1 ^= g_dll_sums[/* ID of the DLL this function is from */];

    uint8_t permutation[32] = { ... constant ... };
    uint8_t working_state[32] = {0};

    for (int i = 0; i < 32; i += 1)
        working_state[i] = arg1[permutation[i]];

    for (int i = 0; i < 32; i += 1)
        arg1[i] = working_state[i];
}

And the last type is a whitened modular exponentiation (by square-and-multiply) modulo $2^{256}$:

// Exponentiation (pseudocode)
void f41689142231683650251(uint8_t* arg1)
{
    *(uint32_t*)arg1 ^= g_dll_sums[/* ID of the DLL this function is from */];
    BigUint256 exponent = { ... constant ... };

    BigUint256 input = biguint256_from_bytes(arg1);
    BigUint256 parity = biguint256_bitwise_and(input, 0x1);

    // Force odd integer
    input = biguint256_bitwise_or(input, 0x1);
    BigUint256 result = biguint256_pow(input, exponent);

    // Copy parity from input to result
    BigUint256 result_p = biguint256_set_lsb(parity);

    biguint256_to_bytes(result_p, arg1);
}

Trivially, both the substitution and permutation operations are reversible (assuming the current dll load sums are known, which they are). Typically, in symmetric cryptography, these two operations are used together with a non-linear operation (such as adding subkeys to the state) to make so-called substitution-permutation network (SPN) ciphers. One ubiquitous example of such a cipher is of course Rijndael, standardized as the AES. For convenience, I will use the term SPN to refer to this process of mixing up the input using the three operations described above.

In this case, however, it turns out that the modular exponentiation step is reversible precisely because the code forces inputs to be odd (odd numbers and only odd numbers are invertible mod $2^n$).

Knowing this, it's clear that we can invert the first part of the check function, i.e. the SPN. Let's see how the rest of check works. After all of the "rounds" of the SPN are done, some constant values are written onto the stack and consequently a short for-loop modifies these constants using the license buffer modified by the SPN. Analyzing this loop straight from the disassembly (as Binja struggled with the sbb instruction), I figured out that a state of 16 128-bit numbers was being xored with the SPN output interpreted as 4 64-bit words instead of 32 individual bytes. At the same time, the 16 resulting u128s are checked against mystery_thing_1, making the function short-circuit and return 0 if any of the state u128s compare above or equal.

uint128_t mystery_thing_1 = 0xd83146b153175933;
int64_t mystery_thing_2 = 0x559d6e12e849596b;

uint128_t result[0x10];
uint8_t idk[0x100];
uint8_t idk_2[0x100];
uint64_t idk_3[0x20];

uint128_t state[16] = {
    0xf98efef9b4d91f6e,
    0x9b6a4c80b5b1f2e8,
    0x2df308609a576a8d,
    0x2602dc84e56fc8d7,
    0x2d73f4fbb5fd9583,
    0xbdf9a047befdcc6b,
    0x59a762c00aee2bc2,
    0x1b3d7791163b4ca4,
    0x1c1c29536ee6d72c,
    0x7d0887fe75684bcf,
    0x34dedfb47c2283a0,
    0x4262f2f39e547f89,
    0x2eac87236b3e6041,
    0x4299e4f3195e3695,
    0xe77d5389e61f24ac,
    0x4d458a85909ea355,
};

for (int32_t i = 0; i < 16; i += 1)
{
    uint128_t state_u128 = state[i];
    uint128_t arg_u128 = promote_u128(((uint64_t *)arg1)[i % 4]);

    state[i] = state_u128 ^ arg_u128;
    if (state[i] >= mystery_thing_1)
        return 0;
}

Next, the mystery_thing_1 is actually always passed as the 2nd argument to the function that is being called repeatedly. At this point, I just decided to treat it as a black-box and observe input-output relationships. Through this, I determined that it computed the remainder after division (a.k.a. modulo) of the first argument by the second. So mystery_thing_1 is really just a modulus.

Whenever there's a modulus, an exponent is likely not too far away. Seeing the pattern of reading mystery_thing_2 bit by bit and doing something if the bit was set, I suspected the nested loop of doing some modular exponentiation. Since I had a large part of the check procedure figured out, I decided to try to let my LLM guess the rest again. I gave it this amalgamation of my own notes as well as Binja and IDA decompiler outputs.

bool check(uint8_t arg1[32])
{
    SPN(arg1); // Encrypts arg1 in place, but I know how to reverse this.

    uint128_t modulus = 0xd83146b153175933; // formerly named {thres_hi, thres_lo}
    int64_t exponent = 0x559d6e12e849596b;

    uint128_t result[0x10]; // &_Buf1[0]
    uint8_t idk[0x100]; // &_Buf1[0x100]
    uint8_t idk_2[0x100]; // &_Buf1[0x200]
    uint64_t idk_3[0x20]; // &_Buf1[0x300]

    // &_Buf1[0x400]
    uint128_t state[16] = {
        0xf98efef9b4d91f6e,
        0x9b6a4c80b5b1f2e8,
        0x2df308609a576a8d,
        0x2602dc84e56fc8d7,
        0x2d73f4fbb5fd9583,
        0xbdf9a047befdcc6b,
        0x59a762c00aee2bc2,
        0x1b3d7791163b4ca4,
        0x1c1c29536ee6d72c,
        0x7d0887fe75684bcf,
        0x34dedfb47c2283a0,
        0x4262f2f39e547f89,
        0x2eac87236b3e6041,
        0x4299e4f3195e3695,
        0xe77d5389e61f24ac,
        0x4d458a85909ea355,
    };

    for (int32_t i = 0; i < 16; i += 1)
    {
        uint128_t state_u128 = state[i];
        uint128_t arg_u128 = promote_u128(((uint64_t *)arg1)[i % 4]);

        state[i] = state_u128 ^ arg_u128;
        if (state[i] >= modulus)
            return 0;
    }

    v110 = 0u;
    v5 = state[0];
    v6 = state[5];
    a1 = (__m128)(state[15] * state[10]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v6);
    *(_OWORD *)a2 = modulus;
    v97 = i128_div_modulo(&a1, (__m128 *)a2);
    v7 = state[6];
    a1 = (__m128)(state[13] * state[11]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v7);
    *(_OWORD *)a2 = modulus;
    v93 = i128_div_modulo(&a1, (__m128 *)a2);
    v8 = state[7];
    a1 = (__m128)(state[14] * state[9]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v8);
    *(_OWORD *)a2 = modulus;
    v89 = i128_div_modulo(&a1, (__m128 *)a2);
    v9 = state[13];
    a1 = (__m128)(state[7] * state[10]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v9);
    *(_OWORD *)a2 = modulus;
    v84 = i128_div_modulo(&a1, (__m128 *)a2);
    v10 = state[14];
    a1 = (__m128)(state[5] * state[11]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v10);
    *(_OWORD *)a2 = modulus;
    v11 = i128_div_modulo(&a1, (__m128 *)a2);
    v12 = state[15];
    a1 = (__m128)(state[6] * state[9]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v12);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v11 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v84 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    v13 = i128_div_modulo(&a1, (__m128 *)a2);
    a1 = (__m128)(*(_OWORD *)&v89 + modulus - *(_OWORD *)&v13);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v93 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v97 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v5);
    *(_OWORD *)a2 = modulus;
    v14 = i128_div_modulo(&a1, (__m128 *)a2);
    a1 = (__m128)(*(_OWORD *)&v14 + *(_OWORD *)&v110);
    *(_OWORD *)a2 = modulus;
    v110 = i128_div_modulo(&a1, (__m128 *)a2);
    v15 = state[1];
    v16 = state[4];
    a1 = (__m128)(state[15] * state[10]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v16);
    *(_OWORD *)a2 = modulus;
    v98 = i128_div_modulo(&a1, (__m128 *)a2);
    v17 = state[6];
    a1 = (__m128)(state[12] * state[11]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v17);
    *(_OWORD *)a2 = modulus;
    v94 = i128_div_modulo(&a1, (__m128 *)a2);
    v18 = state[7];
    a1 = (__m128)(state[14] * state[8]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v18);
    *(_OWORD *)a2 = modulus;
    v90 = i128_div_modulo(&a1, (__m128 *)a2);
    v19 = state[12];
    a1 = (__m128)(state[7] * state[10]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v19);
    *(_OWORD *)a2 = modulus;
    v85 = i128_div_modulo(&a1, (__m128 *)a2);
    v20 = state[14];
    a1 = (__m128)(state[4] * state[11]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v20);
    *(_OWORD *)a2 = modulus;
    v21 = i128_div_modulo(&a1, (__m128 *)a2);
    v22 = state[15];
    a1 = (__m128)(state[6] * state[8]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v22);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v21 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v85 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    v23 = i128_div_modulo(&a1, (__m128 *)a2);
    a1 = (__m128)(*(_OWORD *)&v90 + modulus - *(_OWORD *)&v23);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v94 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v98 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v15);
    *(_OWORD *)a2 = modulus;
    v24 = i128_div_modulo(&a1, (__m128 *)a2);
    a1 = (__m128)(*(_OWORD *)&v110 + modulus - *(_OWORD *)&v24);
    *(_OWORD *)a2 = modulus;
    v110 = i128_div_modulo(&a1, (__m128 *)a2);
    v25 = state[2];
    v26 = state[4];
    a1 = (__m128)(state[15] * state[9]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v26);
    *(_OWORD *)a2 = modulus;
    v99 = i128_div_modulo(&a1, (__m128 *)a2);
    v27 = state[5];
    a1 = (__m128)(state[12] * state[11]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v27);
    *(_OWORD *)a2 = modulus;
    v95 = i128_div_modulo(&a1, (__m128 *)a2);
    v28 = state[7];
    a1 = (__m128)(state[13] * state[8]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v28);
    *(_OWORD *)a2 = modulus;
    v91 = i128_div_modulo(&a1, (__m128 *)a2);
    v29 = state[12];
    a1 = (__m128)(state[7] * state[9]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v29);
    *(_OWORD *)a2 = modulus;
    v86 = i128_div_modulo(&a1, (__m128 *)a2);
    v30 = state[13];
    a1 = (__m128)(state[4] * state[11]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v30);
    *(_OWORD *)a2 = modulus;
    v31 = i128_div_modulo(&a1, (__m128 *)a2);
    v32 = state[15];
    a1 = (__m128)(state[5] * state[8]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v32);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v31 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v86 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    v33 = i128_div_modulo(&a1, (__m128 *)a2);
    a1 = (__m128)(*(_OWORD *)&v91 + modulus - *(_OWORD *)&v33);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v95 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v99 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v25);
    *(_OWORD *)a2 = modulus;
    v34 = i128_div_modulo(&a1, (__m128 *)a2);
    a1 = (__m128)(*(_OWORD *)&v34 + *(_OWORD *)&v110);
    *(_OWORD *)a2 = modulus;
    v110 = i128_div_modulo(&a1, (__m128 *)a2);
    v35 = state[3];
    v36 = state[4];
    a1 = (__m128)(state[14] * state[9]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v36);
    *(_OWORD *)a2 = modulus;
    v100 = i128_div_modulo(&a1, (__m128 *)a2);
    v37 = state[5];
    a1 = (__m128)(state[12] * state[10]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v37);
    *(_OWORD *)a2 = modulus;
    v96 = i128_div_modulo(&a1, (__m128 *)a2);
    v38 = state[6];
    a1 = (__m128)(state[13] * state[8]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v38);
    *(_OWORD *)a2 = modulus;
    v92 = i128_div_modulo(&a1, (__m128 *)a2);
    v39 = state[12];
    a1 = (__m128)(state[6] * state[9]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v39);
    *(_OWORD *)a2 = modulus;
    v87 = i128_div_modulo(&a1, (__m128 *)a2);
    v40 = state[13];
    a1 = (__m128)(state[4] * state[10]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v40);
    *(_OWORD *)a2 = modulus;
    v41 = i128_div_modulo(&a1, (__m128 *)a2);
    v42 = state[14];
    a1 = (__m128)(state[5] * state[8]);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v42);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v41 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v87 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    v88 = i128_div_modulo(&a1, (__m128 *)a2);
    a1 = (__m128)(*(_OWORD *)&v92 + modulus - *(_OWORD *)&v88);
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v96 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&v100 + *(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2));
    *(_OWORD *)a2 = modulus;
    a1 = (__m128)(*(_OWORD *)&i128_div_modulo(&a1, (__m128 *)a2) * v35);
    *(_OWORD *)a2 = modulus;
    v101 = i128_div_modulo(&a1, (__m128 *)a2);
    a1 = (__m128)(*(_OWORD *)&v110 + modulus - *(_OWORD *)&v101);
    *(_OWORD *)a2 = modulus;
    v110 = i128_div_modulo(&a1, (__m128 *)a2);

    if ( *(_OWORD *)&v110 == 0 )
        return 0;

    idk_3[0x0] = 1;
    idk_3[0x1] = 0;
    idk_3[0x2] = 0;
    idk_3[0x3] = 0;
    idk_3[0x4] = 0;
    idk_3[0x5] = 0;
    idk_3[0x6] = 0;
    idk_3[0x7] = 0;
    idk_3[0x8] = 0;
    idk_3[0x9] = 0;
    idk_3[0xa] = 1;
    idk_3[0xb] = 0;
    idk_3[0xc] = 0;
    idk_3[0xd] = 0;
    idk_3[0xe] = 0;
    idk_3[0xf] = 0;
    idk_3[0x10] = 0;
    idk_3[0x11] = 0;
    idk_3[0x12] = 0;
    idk_3[0x13] = 0;
    idk_3[0x14] = 1;
    idk_3[0x15] = 0;
    idk_3[0x16] = 0;
    idk_3[0x17] = 0;
    idk_3[0x18] = 0;
    idk_3[0x19] = 0;
    idk_3[0x1a] = 0;
    idk_3[0x1b] = 0;
    idk_3[0x1c] = 0;
    idk_3[0x1d] = 0;
    idk_3[0x1e] = 1;
    idk_3[0x1f] = 0;

    __builtin_memset(idk_2, 0, 0x100);
    __builtin_memset(idk, 0, 0x100);

    // No-op? Copies state[0..16] to itself...
    for (int32_t i = 0; i < 16; i++)
    {
        uint64_t* rax_830 = &_Buf1[(16 * i) + 0x400];
        uint64_t* rcx_847 = &_Buf1[(16 * i) + 0x400];
        rcx_847[0] = rax_830[0];
        rcx_847[1] = rax_830[1];
    }

    for (int32_t i_2 = 0; i_2 <= 63; i_2 += 1)
    {
        if ((int32_t)(exponent >> (uint8_t)i_2) & 1)
        {
            for (int32_t j = 0; j <= 3; j += 1)
            {
                for (int32_t k = 0; k <= 3; k += 1)
                {
                    void* rax_842 = &_Buf1[((int64_t)(k + (j << 2)) << 4) + 0x100];
                    *(uint64_t*)rax_842 = 0;
                    *(uint64_t*)((char*)rax_842 + 8) = 0;

                    for (int32_t var_60_1 = 0; var_60_1 <= 3; var_60_1 += 1)
                    {
                        void* rax_850 = &_Buf1[((int64_t)(k + (j << 2)) << 4) + 0x100];
                        int64_t rsi_25 = *(uint64_t*)rax_850;
                        int64_t rdi_25 = *(uint64_t*)((char*)rax_850 + 8);
                        void* rax_858 = &_Buf1[((int64_t)(var_60_1 + (j << 2)) << 4) + 0x300];
                        int64_t rax_859 = *(uint64_t*)rax_858;
                        void* rcx_855 = &_Buf1[((int64_t)(k + (var_60_1 << 2)) << 4) + 0x200];
                        int64_t rcx_856 = *(uint64_t*)rcx_855;

                        int64_t rdx_329 = HIGHQ(rax_859 * rcx_856);
                        int64_t rax_860 = LOWQ(rax_859 * rcx_856);
                        int64_t rcx_857 =
                            *(uint64_t*)((char*)rcx_855 + 8)
                            * rax_859 +
                            *(uint64_t*)((char*)rax_858 + 8)
                            * rcx_856 + rdx_329;

                        var_5c8 = rax_860;
                        int64_t var_5c0_77 = rcx_857;
                        var_5d8 = thres_lo;
                        int64_t var_5d0_77 = thres_hi;
                        int128_t zmm0_77 = u128_modulo(&var_5c8, &var_5d8);
                        int64_t r8_117 = (uint64_t)zmm0_77;
                        void* rcx_864 = &_Buf1[((int64_t)((j << 2) + k) << 4) + 0x100];
                        *(uint64_t*)rcx_864 = rsi_25 + r8_117;
                        *(uint64_t*)((char*)rcx_864 + 8) = rdi_25 + *(uint64_t*)((char*)zmm0_77)[8];
                        void* rax_872 = &_Buf1[((int64_t)(k + (j << 2)) << 4) + 0x100];

                        int64_t rbx_133 = *(uint64_t*)((char*)rax_872 + 8);
                        var_5c8 = *(uint64_t*)rax_872;
                        int64_t var_5c0_78 = rbx_133;
                        var_5d8 = thres_lo;
                        int64_t var_5d0_78 = thres_hi;
                        int128_t zmm0_78 = u128_modulo(&var_5c8, &var_5d8);
                        void* rcx_870 = &_Buf1[((int64_t)((j << 2) + k) << 4) + 0x100];
                        *(uint64_t*)rcx_870 = (uint64_t)zmm0_78;
                        *(uint64_t*)((char*)rcx_870 + 8) = *(uint64_t*)((char*)zmm0_78)[8];
                    }
                }
            }

            for (int32_t j_1 = 0; j_1 < 16; j_1++)
            {
                void* rax_882 = &_Buf1[((int64_t)j_1 << 4) + 0x100];
                int64_t rdx_340 = *(uint64_t*)((char*)rax_882 + 8);
                void* rcx_875 = &_Buf1[((int64_t)j_1 << 4) + 0x300];
                *(uint64_t*)rcx_875 = *(uint64_t*)rax_882;
                *(uint64_t*)((char*)rcx_875 + 8) = rdx_340;
            }
        }
        
        for (int32_t j_2 = 0; j_2 < 4; j_2++)
        {
            for (int32_t k_1 = 0; k_1 < 4; k_1++)
            {
                void* rax_891 = &_Buf1[((int64_t)(k_1 + (j_2 << 2)) << 4) + 0x100];
                *(uint64_t*)rax_891 = 0;
                *(uint64_t*)((char*)rax_891 + 8) = 0;
                
                for (int32_t var_70_1 = 0; var_70_1 < 4; var_70_1++)
                {
                    void* rax_899 = &_Buf1[((int64_t)(k_1 + (j_2 << 2)) << 4) + 0x100];
                    int64_t rsi_27 = *(uint64_t*)rax_899;
                    int64_t rdi_28 = *(uint64_t*)((char*)rax_899 + 8);
                    void* rax_907 = &_Buf1[((int64_t)(var_70_1 + (j_2 << 2)) << 4) + 0x200];
                    int64_t rax_908 = *(uint64_t*)rax_907;
                    void* rcx_882 = &_Buf1[((int64_t)(k_1 + (var_70_1 << 2)) << 4) + 0x200];
                    int64_t rcx_883 = *(uint64_t*)rcx_882;
                    int64_t rdx_345 = HIGHQ(rax_908 * rcx_883);
                    int64_t rax_909 = LOWQ(rax_908 * rcx_883);
                    int64_t rcx_884 =
                        *(uint64_t*)((char*)rcx_882 + 8)
                        * rax_908 +
                        *(uint64_t*)((char*)rax_907 + 8)
                        * rcx_883 + rdx_345;

                    var_5c8 = rax_909;
                    int64_t var_5c0_79 = rcx_884;
                    var_5d8 = thres_lo;
                    int64_t var_5d0_79 = thres_hi;

                    int128_t zmm0_79 = u128_modulo(&var_5c8, &var_5d8);

                    int64_t r8_122 = (uint64_t)zmm0_79;
                    void* rcx_891 = &_Buf1[((int64_t)((j_2 << 2) + k_1) << 4) + 0x100];
                    *(uint64_t*)rcx_891 = rsi_27 + r8_122;
                    *(uint64_t*)((char*)rcx_891 + 8) =
                        rdi_28
                        + *(uint64_t*)((char*)zmm0_79)[8];

                    void* rax_921 = &_Buf1[((int64_t)(k_1 + (j_2 << 2)) << 4) + 0x100];
                    int64_t rbx_138 = *(uint64_t*)((char*)rax_921 + 8);
                    var_5c8 = *(uint64_t*)rax_921;

                    int64_t var_5c0_80 = rbx_138;
                    var_5d8 = thres_lo;
                    int64_t var_5d0_80 = thres_hi;
                    int128_t zmm0_80 = u128_modulo(&var_5c8, &var_5d8);

                    void* rcx_897 = &_Buf1[((int64_t)((j_2 << 2) + k_1) << 4) + 0x100];
                    *(uint64_t*)rcx_897 = (uint64_t)zmm0_80;
                    *(uint64_t*)((char*)rcx_897 + 8) = *(uint64_t*)((char*)zmm0_80)[8];
                }
            }
        }
        
        for (int32_t j_3 = 0; j_3 < 16; j_3++)
        {
            void* rax_931 = &_Buf1[((int64_t)j_3 << 4) + 0x100];
            int64_t rdx_356 = *(uint64_t*)((char*)rax_931 + 8);
            void* rcx_902 = &_Buf1[((int64_t)j_3 << 4) + 0x200];
            *(uint64_t*)rcx_902 = *(uint64_t*)rax_931;
            *(uint64_t*)((char*)rcx_902 + 8) = rdx_356;
        }
    }

    uint128_t reference[16] = {
        0x1F2CCE278F7F0F03,
        0x888A753879E68DAE,
        0x5D9239E3618BFF63,
        0xC435210FB4402532,
        0x2525FDEF8C7D331F,
        0x91946D8C60DFB121,
        0x2BBD94327DE98D3C,
        0x92687B6921C294D9,
        0x9B6D2CD527805891,
        0xC8B953E0B3259F8A,
        0x9940614C1A71E163,
        0x3B7509EA3F34B738,
        0x8D12A5121B46FC6F,
        0x826512EE04D2A7A4,
        0x27E7AF737205BC87,
        0x33371FE0DE4D083E,
    }

    return !memcmp(reference, result, 16 * sizeof(uint128_t));
}

I asked the model to analyze and summarize the semantics of the big block using modular reductions and the nested loop, and it correctly inferred that the initial state (xored with the SPN output) is interpreted as a 4x4 matrix $M$, its determinant is computed modulo modulus (let's call it $p$ for short) and compared to zero, effectively checking if $M$ is invertible in $GF(p)$. If it is not, the check fails.

The nested loop before the end then raises $M$ to the hardcoded exponent $E$ and checks the result against a hardcoded reference $R$. This means that if we are to find the preimage of each of the 10,000 32-byte chunks checked by each of the 10,000 DLLs, we need to:

1. Find the $M \in GL(4, p)$ satisfying $M^E \equiv R \pmod p$ (where $GL(4, p)$ is the multiplicative group of 4x4 matrixes over $GF(p)$),
2. find the SPN output by xoring $M$ with $M'$, where $M'$ is the hardcoded initial matrix,
3. invert the SPN (with the correct DLL load sums) to recover the passing input.

A question that needs addressing is of course how to find the $E$-th root of $R$ in $GF(p)$. This turns out to be much less difficult than it sounds, due to the fact that $G := GL(4, p)$ is a group.

• Because it is a group, we know from Lagrange's theorem that for every $M \in G$, $M^{|G|} = \mathbf I$ (every element raised to the group order equals the group identity).
• If $\gcd (E, |G|) = 1$, then we can find the multiplicative inverse of $E$, i.e. an integer $d$ such that $E \cdot d \equiv 1 \pmod{|G|}$.
• Then $R^d = (M^E)^d = M^{E \cdot d} = M^1 = M$ (implicitly referring to operations in $G$).

This will work as long as $\gcd(E, |G|) = 1$, which is technically not guaranteed, but is almost certain if $E$ and $p$ are chosen at random.

Putting everything together

In theory, we know how to find the correct 32-byte input for each of the 10,000 check functions. What remains to do in theory is to find the correct permutation of the DLLs to get the correct load sums; what remains to do in practice is practically everything.

Fortunately, the assumption from earlier, that the DLL load sums are only ever read and never written by the check functions, seems to be correct based on the previous analysis. This means that their final values are influenced only by the order in which the DLLs are specified in the license, which we now must find.

The problem is essentially a graph-theoretical one, and can be restated as follows:

Given a directed graph $G = (V, E)$, $|V| = 10000$, find a bijection $f: V \rightarrow \{0, \dots, |V| - 1\}$ such that

where $T_v$ is the target sum for node (DLL) $v$ and $u \rightarrow^* v$ means that $v$ is reachable from $u$ (inclusive the situation $u = v$).

Now, as it's rather difficult to solve a graph problem without a graph, let's build one. The nodes (vertexes) will be the DLLs (0...9999) and an edge will go from $v$ to $w$ if DLL $v$ imports symbols from DLL $w$. The below C++ program parses each DLL and its import directory and adds the appropriate edges to the graph. The result it then saved into a JSON file.

#include <cassert>
#include <cstdio>
#include <string>
#include <vector>
#include <windows.h>

void parse_imports(int i, std::vector<int>& out)
{
    char filename[256];
    assert(-1 != sprintf_s(filename, sizeof filename, "%04d.dll", i));

    HMODULE hDll = LoadLibraryA(filename);
    assert(hDll);

    PIMAGE_NT_HEADERS64 pNtHeaders = (PIMAGE_NT_HEADERS64)((BYTE *)hDll + *(DWORD *)((BYTE *)hDll + 0x3C)); 
    assert(pNtHeaders->Signature == 0x00004550);

    DWORD ImportsRva = pNtHeaders->OptionalHeader.DataDirectory[1].VirtualAddress;
    DWORD ImportsSize = pNtHeaders->OptionalHeader.DataDirectory[1].Size;

    PIMAGE_IMPORT_DESCRIPTOR ImportDescriptor = (PIMAGE_IMPORT_DESCRIPTOR)((BYTE *)hDll + ImportsRva);

    for (; ImportDescriptor->Name; ++ImportDescriptor)
    {
        LPCSTR ImportName = (LPCSTR)((BYTE *)hDll + ImportDescriptor->Name);

        if (
            ImportName[0] - '0' > 9 || ImportName[1] - '0' > 9
            || ImportName[2] - '0' > 9 || ImportName[3] - '0' > 9
        )
            continue;

        int import_num = (ImportName[0] - '0') * 1000
            + (ImportName[1] - '0') * 100
            + (ImportName[2] - '0') * 10
            + (ImportName[3] - '0');

        printf("Import graph edge: %04d -> %04d\n", i, import_num);
        out.push_back(import_num);
    }

    CloseHandle(hDll);
}

void dump_graph_to_file(const char *filename, const std::vector<std::vector<int>>& graph)
{
    FILE *fp = fopen(filename, "w");
    assert(fp);
    
    fprintf(fp, "{\n");
    for (int i = 0; i < 10000; ++i)
    {
        fprintf(fp, "    \"%d\": [", i);
        for (int j = 0; j < graph[i].size(); ++j)
        {
            if (j != 0)
                fprintf(fp, ", ");
            fprintf(fp, "%d", graph[i][j]);
        }
        fprintf(fp, i == 9999 ? "]\n" : "],\n");
    }
    fprintf(fp, "}\n");

    fclose(fp);
}

int main()
{
    std::vector<std::vector<int>> graph;
    graph.resize(10000);

    for (int i = 0; i < 10000; ++i)
    {
        parse_imports(i, graph[i]);
    }

    dump_graph_to_file("import_graph.json", graph);
}

Compiling and running the code produces a ~14 MB JSON file encoding the import dependency graph, which we can now reuse in further calculations. A very useful property of this graph is the absence of cycles (there are no two DLLs that import each other, even transitively). In other words, we are dealing with a directed acyclic graph (DAG). This means that we can topologically sort the vertexes and reconstruct the DLL check order (the $f$ bijection) by starting at the sources (vertexes with no incoming edges). For a vertex with no incoming edges, the target value must be exactly equal to the iteration in which it is checked. Once the sources are resolved, we can remove them (adjusting the target weights accordingly) and continue until the whole bijection is found.

Somewhat surprisingly, an LLM-generated Python solver worked first-try (I only wrote the code to verify the correctness of a solution), which is why I wasn't bother to write my own.

def solve_dag(n, edges, targets):
    """
    Solve the reachability-sum assignment problem for a DAG.

    Parameters:
        n        : number of vertices (0..n-1)
        edges    : list of (u,v) directed edges
        targets  : list of target sums per vertex
    Returns:
        ordering : list of vertices in visiting order
    """
    from collections import defaultdict, deque
    import sys
    sys.setrecursionlimit(1_000_000)

    # Build graph
    g = [[] for _ in range(n)]
    rg = [[] for _ in range(n)]
    indeg = [0] * n
    for u, v in edges:
        g[u].append(v)
        rg[v].append(u)
        indeg[v] += 1

    # Topological order
    q = deque([i for i in range(n) if indeg[i]==0])
    topo=[]
    while q:
        u = q.popleft()
        topo.append(u)
        for v in g[u]:
            indeg[v] -= 1
            if indeg[v] == 0:
                q.append(v)
    if len(topo) != n:
        raise ValueError("Graph is not a DAG (cycle detected)")

    # Compute ancestors bitsets (fast with integers)
    ancestors = [0] * n
    for v in topo:
        bits = 0
        for p in rg[v]:
            bits |= ancestors[p]
            bits |= (1 << p)
        ancestors[v] = bits

    # Invert the system: compute A_v
    A = [0]*n
    for v in topo:
        bits = ancestors[v]
        s = 0
        while bits:
            lsb = bits & -bits
            j = lsb.bit_length() - 1
            s += A[j]
            bits ^= lsb
        A[v] = targets[v] - s

    # Check total sum and consistency
    total_sum = n * (n - 1) // 2
    if sum(A) != total_sum:
        print(f"Warning: sum(A) = {sum(A)} != total = {total_sum}")
    for i, a in enumerate(A):
        if a < 0:
            raise ValueError(f"A[{i}] = {a} < 0 (impossible)")

    # Now A[v] are the numbers assigned to vertices directly
    # They must be distinct and cover the right range.
    # Map numbers 0..n-1 to vertices
    used = set(A)
    expected = set(range(0, n))
    if used != expected:
        raise ValueError(f"A not a permutation of {expected}")
    ordering = [None] * n
    for v, a in enumerate(A):
        ordering[a] = v
    return ordering

import json

with open("import_graph.json", "r") as f:
    graph = { int(k): v for k, v in json.load(f).items() }

with open("reference_import_sums.json", "r") as f:
    targets = json.load(f)

edges = []
for v in range(10000):
    for w in graph[v]:
        edges.append((v, w))

ordering = solve_dag(10000, edges, targets)
print(ordering) # [7476, 5402, 4885, 5176, 6815, 7764, 9981, 655, 6606, 7019, ...]

Note: reference_import_sums.json simply has a list of the target values extracted from the EXE.

Parsing check parameters and SPN functions

Theoretically, we've now successfully finished the challenge and can have a deserved rest. But you and I know that's not how this works.

Practically, all that is left is to:

• Parse the modulus, exponent, initial and reference matrixes in each check function,
• parse the sequence of SPN functions called in each check function,
• parse the type of each SPN function and the constant parameter (s-box, permutation, or exponent),
• run the whole check process backwards to recover the valid license.

Parsing check parameters

In the snippet below, I parse the immediate operands of instructions that write the parameters onto the stack using regular expressions (before you say that it's dumb, please realize that I know). This is extremely thin ice, as any instruction byte can happen to be a special regex character, requiring some care to escape them. Thankfully, these instructions and stack offsets are the same across all 10000 DLLs, making our life slightly more bearable.

# pip install pefile
import pefile
import re

Mat4x4 = list[list[int]]

def find_export_rva(pe: pefile.PE, name: str) -> int:
    for exp in pe.DIRECTORY_ENTRY_EXPORT.symbols:
        if exp.name.decode() == name:
            return exp.address
    raise ValueError(f"Export '{name}' not found")

def parse_matrix_encryption_consts(file_data: bytes, pe: pefile.PE) -> tuple[Mat4x4, Mat4x4, int, int]:
    EXPORT_NAME = "_Z5checkPh"

    check_fn_rva = find_export_rva(pe, EXPORT_NAME)
    check_fn_offset = pe.get_offset_from_rva(check_fn_rva)

    fn_end_pattern = bytes.fromhex("85C00F94C00FB6C04881C4080600005B5E5F415C415D415E415F5DC3")
    check_fn_offset_end = file_data.find(fn_end_pattern, check_fn_offset)
    assert check_fn_offset_end > check_fn_offset

    fn_bytes = file_data[check_fn_offset:check_fn_offset_end]

    """
    Prime modulus:

    .text:000000034222DCA1 48 B8 33 59 17 53 B1 46 31 D8    mov     rax, 0D83146B153175933h
    .text:000000034222DCAB BA 00 00 00 00                   mov     edx, 0
    .text:000000034222DCB0 48 89 85 40 05 00 00             mov     [rbp+540h], rax
    """
    prime_re = re.compile(b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x40\x05\x00\x00", re.DOTALL)   

    """
    Exponent:

    .text:000000034222DCBE 48 B8 6B 59 49 E8 12 6E 9D 55    mov     rax, 559D6E12E849596Bh
    .text:000000034222DCC8 48 89 85 38 05 00 00             mov     [rbp+538h], rax
    """
    exponent_re = re.compile(b"\x48\xB8(.{8})\x48\x89\x85\x38\x05\x00\x00", re.DOTALL)   

    """
    Initial matrix:

    .text:000000034222DCCF 48 B8 6E 1F D9 B4 F9 FE 8E F9    mov     rax, 0F98EFEF9B4D91F6Eh
    .text:000000034222DCD9 BA 00 00 00 00                   mov     edx, 0
    .text:000000034222DCDE 48 89 85 10 04 00 00             mov     [rbp+410h], rax
    .text:000000034222DCE5 48 89 95 18 04 00 00             mov     [rbp+418h], rdx
    .text:000000034222DCEC 48 B8 E8 F2 B1 B5 80 4C 6A 9B    mov     rax, 9B6A4C80B5B1F2E8h
    .text:000000034222DCF6 BA 00 00 00 00                   mov     edx, 0
    .text:000000034222DCFB 48 89 85 20 04 00 00             mov     [rbp+420h], rax
    .text:000000034222DD02 48 89 95 28 04 00 00             mov     [rbp+428h], rdx
    .text:000000034222DD09 48 B8 8D 6A 57 9A 60 08 F3 2D    mov     rax, 2DF308609A576A8Dh
    .text:000000034222DD13 BA 00 00 00 00                   mov     edx, 0
    .text:000000034222DD18 48 89 85 30 04 00 00             mov     [rbp+430h], rax
    .text:000000034222DD1F 48 89 95 38 04 00 00             mov     [rbp+438h], rdx
    (...)
    """
    initial_re = re.compile(
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x10\x04\x00\x00\x48\x89\x95\x18\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x20\x04\x00\x00\x48\x89\x95\\\x28\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x30\x04\x00\x00\x48\x89\x95\x38\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x40\x04\x00\x00\x48\x89\x95\x48\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x50\x04\x00\x00\x48\x89\x95\x58\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x60\x04\x00\x00\x48\x89\x95\x68\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x70\x04\x00\x00\x48\x89\x95\x78\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x80\x04\x00\x00\x48\x89\x95\x88\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x90\x04\x00\x00\x48\x89\x95\x98\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xA0\x04\x00\x00\x48\x89\x95\xA8\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xB0\x04\x00\x00\x48\x89\x95\xB8\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xC0\x04\x00\x00\x48\x89\x95\xC8\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xD0\x04\x00\x00\x48\x89\x95\xD8\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xE0\x04\x00\x00\x48\x89\x95\xE8\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xF0\x04\x00\x00\x48\x89\x95\xF8\x04\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x00\x05\x00\x00\x48\x89\x95\x08\x05\x00\x00",
        re.DOTALL
    )

    """
    Reference matrix:

    .text:00000003422304C2 48 B8 03 0F 7F 8F 27 CE 2C 1F    mov     rax, 1F2CCE278F7F0F03h
    .text:00000003422304CC BA 00 00 00 00                   mov     edx, 0
    .text:00000003422304D1 48 89 45 10                      mov     [rbp+10h], rax
    .text:00000003422304D5 48 89 55 18                      mov     [rbp+18h], rdx
    .text:00000003422304D9 48 B8 AE 8D E6 79 38 75 8A 88    mov     rax, 888A753879E68DAEh
    .text:00000003422304E3 BA 00 00 00 00                   mov     edx, 0
    .text:00000003422304E8 48 89 45 20                      mov     [rbp+20h], rax
    .text:00000003422304EC 48 89 55 28                      mov     [rbp+28h], rdx
    .text:00000003422304F0 48 B8 63 FF 8B 61 E3 39 92 5D    mov     rax, 5D9239E3618BFF63h
    .text:00000003422304FA BA 00 00 00 00                   mov     edx, 0
    .text:00000003422304FF 48 89 45 30                      mov     [rbp+30h], rax
    .text:0000000342230503 48 89 55 38                      mov     [rbp+38h], rdx
    (...)
    """
    reference_re = re.compile(
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x45\x10\x48\x89\x55\x18"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x45\x20\x48\x89\x55\\\x28"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x45\x30\x48\x89\x55\x38"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x45\x40\x48\x89\x55\x48"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x45\x50\x48\x89\x55\x58"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x45\x60\x48\x89\x55\x68"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x45\x70\x48\x89\x55\x78"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x80\x00\x00\x00\x48\x89\x95\x88\x00\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x90\x00\x00\x00\x48\x89\x95\x98\x00\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xA0\x00\x00\x00\x48\x89\x95\xA8\x00\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xB0\x00\x00\x00\x48\x89\x95\xB8\x00\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xC0\x00\x00\x00\x48\x89\x95\xC8\x00\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xD0\x00\x00\x00\x48\x89\x95\xD8\x00\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xE0\x00\x00\x00\x48\x89\x95\xE8\x00\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\xF0\x00\x00\x00\x48\x89\x95\xF8\x00\x00\x00"
        b"\x48\xB8(.{8})\xBA\x00\x00\x00\x00\x48\x89\x85\x00\x01\x00\x00\x48\x89\x95\x08\x01\x00\x00",
        re.DOTALL
    )

    prime_match = re.search(prime_re, fn_bytes)
    exponent_match = re.search(exponent_re, fn_bytes)
    initial_match = re.search(initial_re, fn_bytes)
    reference_match = re.search(reference_re, fn_bytes)

    if any(x is None for x in (prime_match, exponent_match, initial_match, reference_match)):
        raise ValueError(f"Could not extract all params from function machine code: {(prime_match, exponent_match, initial_match, reference_match) = }")

    prime = int.from_bytes(prime_match.group(1), "little")
    exponent = int.from_bytes(exponent_match.group(1), "little")
    initial_matrix = [int.from_bytes(initial_match.group(i + 1), "little") for i in range(16)]
    reference_matrix = [int.from_bytes(reference_match.group(i + 1), "little") for i in range(16)]

    def reshape_4x4(nums):
        return [nums[0:4], nums[4:8], nums[8:12], nums[12:16]]

    return reshape_4x4(initial_matrix), reshape_4x4(reference_matrix), exponent, prime