->*

Challenge 8 ("FlareAuthenticator")

Description

We recovered a legacy authenticator from an old hard disk, but the password has been lost and we only remember that there was a single password to unlock it. We need your help to analyze the program and find a way to get back in. Can you recover the password?

Writeup

The archive contains these files:

vcruntime140_1.dll
vcruntime140.dll
run.bat
qwindows.dll
Qt6Widgets.dll
Qt6Gui.dll
Qt6Core.dll
msvcp140_2.dll
msvcp140_1.dll
msvcp140.dll
FlareAuthenticator.exe

I wanted to make sure the focus of the challenge was on the FlareAuthenticator.exe binary, so I checked the hashes and signatures of all the DLLs to verify they haven't been tampered with in any way. All signatures matched.

Next, the run.bat script only sets up a required environment variable and runs the EXE.

@echo off
set QT_QPA_PLATFORM_PLUGIN_PATH=%~dp0
start %~dp0\FlareAuthenticator.exe

The focus is therefore really on the authenticator executable, which is a GUI application based on the Qt6 framework (proprietary, but the de facto standard for native cross-platform applications, like IDA Pro for one instance).

The GUI of the authenticator app

The catch with frameworks like Qt6 in terms of reversing is the famous inversion of control (IoC, no, not that IoC) design principle. What this means to say is that instead of the application programmer being reponsible for the core control flow of the program, with ocasional calls to library functions, the opposite is true: The framework handles the "core" of the application, while programmer-defined attributes, styles, events and callbacks are accessed and handled from within the framework's event loop.

Practically, it means that very little significant work takes place in user code before the application calls QApplication::exec(void) at preferred virtual address (PVA) 0x140075442.

.text:0000000140075442    call    rax    ; QApplication::exec(void)

Because I'm firstly not that familiar with Qt internals and how, when or where the connections between objects, slots and callbacks are created, I reached for a tool which I haven't used in quite some time: Cheat Engine.

Cheat Engine is an amazing little tool; primarily developed as a process memory scanner capable of finding interesting data in videogame processes and tweaking them to the user's liking, it also features disassembling, debugging and memory patching capabilities, scripting with Lua, and much more. In this case, my reason for wanting to use it was simple. I would dynamically find the address of whatever storage object contained the user input, which would allow me to place a hardware breakpoint on some variable (either the length of the input or one of the input digits) and find the address of instructions that write to it. From there, I could trace execution back to the point where control flow was handed over from Qt6 to user code, finding the appropriate event handler.

Using this strategy, I found the function at PVA 0x140088520, which is called from Qt6Core.dll. This function contains a call rax instruction that dispatches the event to different handlers based on the event "type" (this may not be proper Qt6 terminology):

When any GUI number button (0-9) is clicked, rax is 0x140012E50,
when the delete button (DEL) is clicked, rax is 0x14002F8C0,
when the OK button is clicked, rax is 0x1400202B0,
and finally, when either return, backspace or any number key is pressed on the keyboard, rax points to QAbstractButton::click(void), which eventually calls this function again. (In other words, key presses are hard-wired to be translated into button clicks).

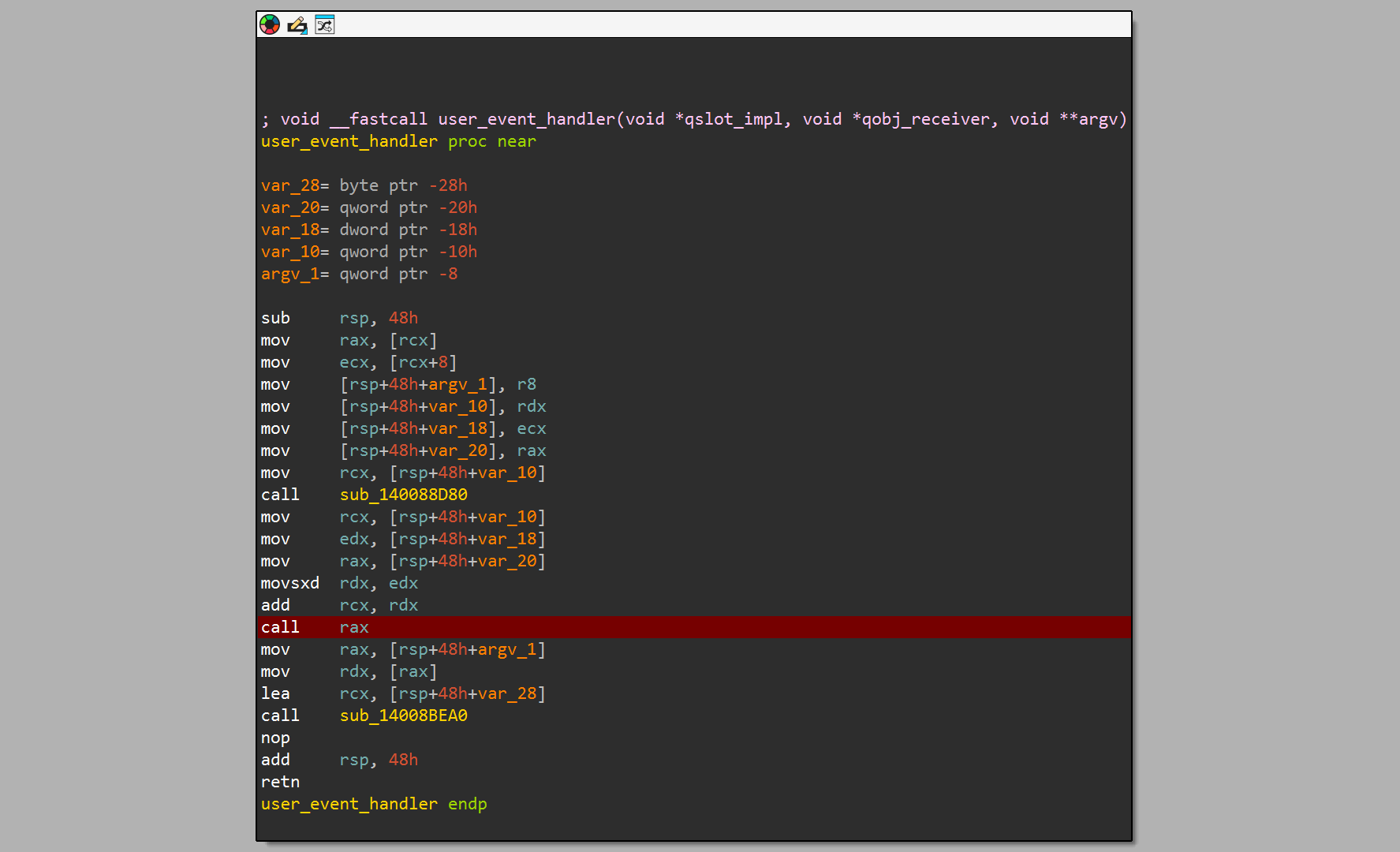
Disassembly of user-defined event handler

At this point I decided to just walk through the OK handler and see what the general control flow looks like. The code of most of the user functions is obfuscated using opaque predicates and jumps to dynamically computed addresses. In the screenshot below, one such instance is shown, where an opaque predicate is used to compute the jump target, which is actually constant.

Control flow obfuscation in user code

This kind of control flow graph (CFG) obfuscation could be removed using symbolic backwards slicing, but as usual, such an undertaking was not worth the effort, compared to just noting down the jump targets and dealing with them manually (there is actually not that much code that needs to be analyzed). One helpful thing for IDA users is that when you put an address (or address name) into a comment in IDA (like on the last instruction in the screenshot above), you can then double click it (or press the return key with the cursor on it) to jump to that address. While I would like an easy way to add instruction cross-references in IDA (i.e. force the jmp rax to be connected to the target address in IDA's graph view), without having to write a whole ass IDA plugin with an IDP hook, this doesn't seem to be possible, which is annoying for sure, but not critical for this challenge.

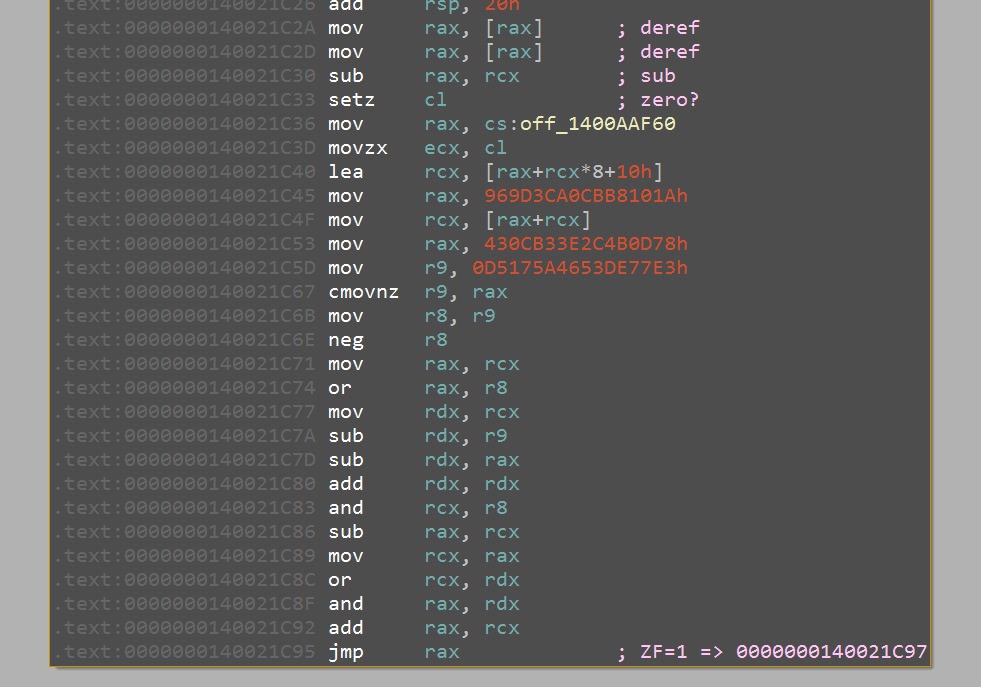
Using this method, I identified the crucial conditional jump at PVA 0x14002211D, which ultimately makes the decision whether to display an error message or a success message. Below are screenshots of the behaviour when ZF=1 and ZF=0, respectively.

The message shown when ZF=1

The message shown when ZF=0

Tracing back the data involved in this check, I found out that a particular QWORD on the stack (found at offset 0x78 of the QWidget object passed as an argument to the handler) is compared to a constant value 0x0BC42D5779FEC401 and the "success" branch is (unsurprisingly) taken when both operands are equal.

.text:00000001400202B0 push    rbp
.text:00000001400202B1 push    r15
.text:00000001400202B3 push    r14
.text:00000001400202B5 push    r13
.text:00000001400202B7 push    r12
.text:00000001400202B9 push    rsi
.text:00000001400202BA push    rdi
.text:00000001400202BB push    rbx
.text:00000001400202BC mov     eax, 2998h
.text:00000001400202C1 call    __alloca_probe
.text:00000001400202C6 sub     rsp, rax
.text:00000001400202C9 lea     rbp, [rsp+80h]
...
.text:00000001400202DC mov     [rbp+2950h+p_qwidget], rcx
...
.text:0000000140021E09 mov     rcx, [rbp+2950h+p_qwidget]   ; read
.text:0000000140021E10 add     rsp, 20h
.text:0000000140021E14 mov     rax, [rax]
.text:0000000140021E17 mov     [rax+30h], rcx               ; writes p_qwidget_2
.text:0000000140021E1B mov     rax, [rbp+2950h+p_qwidget_2] ; read
...
.text:0000000140021E29 mov     rax, [rax+78h]               ; deref +0x78
.text:0000000140021E2D mov     rcx, 0BC42D5779FEC401h
.text:0000000140021E37 sub     rax, rcx
.text:0000000140021E3A setz    al                           ; compare with constant
.text:0000000140021E3D mov     [rbp+2950h+comparison_with_qwidget_plus_0x78_iszero], al
...
.text:0000000140022115 mov     al, [rbp+2950h+comparison_with_qwidget_plus_0x78_iszero]
.text:000000014002211B test    al, 1
.text:000000014002211D jnz     short loc_140022124

Now, to trace back the origin of this mystery value, I utilized the fact that it stayed in the same memory location between attempts (the program lets you input a password repeatedly without quitting) and set a hardware breakpoint on that address.

First, I observed in being reset to 0, still inside the OK button handler. Assuming it starts at zero and ends up with some random looking value, it's not far-fetched to call this value some checksum of the input.

.text:000000014000FAA5 mov     [rcx+78h], rax    ; rax = 0

The next place that updates the checksum is inside the input append handler mentioned earlier, where it is read and somehow combined with another value (var_C78).

.text:0000000140016AC9 mov     r9, [rbp+0FC0h+var_C78]
.text:0000000140016AD0 mov     rdx, [rax+78h]
.text:0000000140016AD4 mov     rcx, r9
.text:0000000140016AD7 not     rcx
.text:0000000140016ADA mov     r8, rdx
.text:0000000140016ADD not     r8
.text:0000000140016AE0 or      r8, rcx
.text:0000000140016AE3 mov     rcx, rdx
.text:0000000140016AE6 add     rcx, r9
.text:0000000140016AE9 lea     r8, [r8+rcx+1]
.text:0000000140016AEE or      rdx, r9
.text:0000000140016AF1 sub     rcx, rdx
.text:0000000140016AF4 mov     rdx, rcx
.text:0000000140016AF7 or      rdx, r8
.text:0000000140016AFA and     rcx, r8
.text:0000000140016AFD add     rcx, rdx
.text:0000000140016B00 mov     [rax+78h], rcx

Writing out and simplifying the expression in a high-level C-like syntax, we get something like this:

\begin{align*} \texttt{r8} &:= ((\lnot \texttt{checksum}) \mid (\lnot \texttt{var\_{C79}})) + \texttt{checksum} + \texttt{var\_C78} + 1 \\ \texttt{rcx} &:= \texttt{checksum} + \texttt{var\_C78} - (\texttt{checksum} \mid \texttt{var\_C78}) \\ \texttt{rdx} &:= (\texttt{checksum} + \texttt{var\_C78} - (\texttt{checksum} \mid \texttt{var\_C78})) \\ &\quad\mid (((\lnot \texttt{checksum}) \mid (\lnot \texttt{var\_C79})) + \texttt{checksum} + \texttt{var\_C78} + 1) \\ \texttt{checksum} &:= (\texttt{rcx}\ \&\ \texttt{r8}) + \texttt{rdx} \end{align*}

(where $\mid$ , $\&$ and $\lnot$ are bitwise or, and and not operations respectively, and $+$ and $-$ are taken modulo $2^{64}$ ). Setting $C = \texttt{checksum}$ and $V = \texttt{var\_C79}$ for brevity, this is equivalent to

\begin{align*} \texttt{checksum} := &\ ((C + V - (C \mid V))\ \&\ (((\lnot C) \mid (\lnot V)) + C + V + 1)) \\ &\quad +\ ((C + V - (C \mid V)) \mid (((\lnot C) \mid (\lnot V)) + C + V + 1)) \end{align*}

and using the identity $(x\ \&\ y) + (x \mid y) = x + y$ , the expression further simplifies to

\begin{align*} \texttt{checksum} := &\ \texttt{checksum} + \texttt{var\_C78} - (\texttt{checksum} \mid \texttt{var\_C78}) \\ &\quad +\ ((\lnot \texttt{checksum}) \mid (\lnot \texttt{var\_C79})) + \texttt{checksum} + \texttt{var\_C78} + 1 \end{align*}

and further, due to the same identity as above and De Morgan's law,

\begin{align*} \texttt{checksum} := &\ (\texttt{checksum}\ \&\ \texttt{var\_C78}) \\ &\quad +\ (\lnot (\texttt{checksum}\ \&\ \texttt{var\_C79})) + \texttt{checksum} + \texttt{var\_C78} + 1 \end{align*}

or equivalently

\begin{align*} \texttt{checksum} := &\ (\texttt{checksum}\ \&\ \texttt{var\_C78}) + (\lnot (\texttt{checksum}\ \&\ \texttt{var\_C79})) + 1 \\ &\quad +\ \texttt{checksum} + \texttt{var\_C78} \end{align*}

and thus, because of $-x = \lnot x + 1$ ,

\texttt{checksum} := 0 + \texttt{checksum} + \texttt{var\_C78},

written more idiomatically in C as checksum += var_C78.

Reversing the checksum logic

So, we know that for each of the 25 digits making up the password, a checksum, initialized to 0, is incremented in the handler function by some value in var_C78. Let's trace it back to see how it is computed.

A simple Alt + Up arrow in IDA on var_C78 reveals that it is written here:

.text:0000000140016711 mov     rdx, [rbp+0FC0h+var_BC0]
.text:0000000140016718 mov     al, [rbp+0FC0h+var_C01]
.text:000000014001671E movsx   r9d, al
.text:0000000140016722 mov     eax, r9d
.text:0000000140016725 not     eax
.text:0000000140016727 mov     r11d, edx
.text:000000014001672A not     r11d
.text:000000014001672D or      r11d, eax
.text:0000000140016730 mov     eax, edx
.text:0000000140016732 add     eax, r9d
.text:0000000140016735 mov     r10d, eax
.text:0000000140016738 mov     r8d, r11d
.text:000000014001673B lea     r8d, [r8+r10+1]
.text:0000000140016740 or      edx, r9d
.text:0000000140016743 sub     eax, edx
.text:0000000140016745 mov     edx, eax
.text:0000000140016747 or      edx, r8d
.text:000000014001674A and     eax, r8d
.text:000000014001674D add     eax, edx
.text:000000014001674F mov     dx, ax
.text:0000000140016752 mov     rax, cs:off_1400BFE40
.text:0000000140016759 mov     r8, 64ED705730BC6591h
.text:0000000140016763 add     rax, r8
.text:0000000140016766 call    rax ; sub_140081760(&qwidget, var_BC0 + var_C01)
.text:0000000140016768 mov     rcx, rax
.text:000000014001676B mov     rax, [rbp+0FC0h+var_C00]
.text:0000000140016772 imul    rax, rcx
.text:0000000140016776 mov     [rbp+0FC0h+var_C78], rax

or in C-like syntax (with deobfuscated arithmetics):

var_C78 = var_C00 * sub_140081760(&qwidget, var_BC0 + var_C01)

where var_C00 can be, analogously to before, traced back to

.text:0000000140015E77 mov     rcx, [rbp+0FC0h+var_948]
.text:0000000140015E7E mov     dx, [rbp+0FC0h+var_B82]
.text:0000000140015E85 mov     rax, cs:off_1400A87D0
.text:0000000140015E8C mov     r8, 0A2B91DB25EE5355Dh
.text:0000000140015E96 add     rax, r8
.text:0000000140015E99 call    rax ; sub_140081760(&qwidget, i + 1)
.text:0000000140015E9B mov     rcx, [rbp+0FC0h+var_948]
.text:0000000140015EA2 mov     [rbp+0FC0h+var_C00], rax

so in total, we have the following formula.

checksum += sub_140081760(&qwidget, var_B82) * sub_140081760(&qwidget, var_BC0 + var_C01)

We could continue the same way to reverse-engineer variables var_B82, var_BC0 and var_C01, but if you simply break at the function calls in each iteration (let's say entering digits "69420"), you will observe these calls:

checksum += sub_140081760(&qwidget, 0x1) * sub_140081760(&qwidget, 0x0136)
checksum += sub_140081760(&qwidget, 0x2) * sub_140081760(&qwidget, 0x0239)
checksum += sub_140081760(&qwidget, 0x3) * sub_140081760(&qwidget, 0x0334)
checksum += sub_140081760(&qwidget, 0x4) * sub_140081760(&qwidget, 0x0432)
checksum += sub_140081760(&qwidget, 0x5) * sub_140081760(&qwidget, 0x0530)

It is not hard to see that the function is simply called with the length of the input so far for the first time and then with the length to the input shifted by 1 byte to the left and added to the input character (0x30 to 0x39 is ASCII '0'-'9').

Next, I wanted to see if sub_140081769 a) was deterministic and b) accessed the QWidget * pointer at all. I decided to let it run normally once, taking note of the second argument and the output, then forcing the RIP back to the call and running it again with rcx = 0 and the same rdx. The result was the same and the program didn't crash due to a null pointer dereference, so I assumed this was a QWidget method that didn't really use this, but only computed some deterministic function.

Because I really didn't want to reverse-engineer this computation, I cached the result for all possible inputs and dumped this to a file. I did this in precisely the same way as I just mentioned, only automated with some ChatGPT-generated IDAPython.

import ida_dbg
import ida_idd
import ida_kernwin

def set_regs_step_over(rax_value, rdx_value, rip_value, wait_timeout_seconds=5):
    if not ida_dbg.is_debugger_on():
        raise RuntimeError("Debugger is not active. Start/attach to a process first.")

    ok = ida_dbg.set_reg_val("rax", rax_value)
    if not ok:
        raise RuntimeError("Failed to set RAX.")
    ok = ida_dbg.set_reg_val("rdx", rdx_value)
    if not ok:
        raise RuntimeError("Failed to set RDX.")
    ok = ida_dbg.set_reg_val("rip", rip_value)
    if not ok:
        raise RuntimeError("Failed to set RIP.")

    if not ida_dbg.step_over():
        raise RuntimeError("Failed to start step-over.")

    wait_timeout = int(wait_timeout_seconds) if wait_timeout_seconds is not None else -1
    ev = ida_dbg.wait_for_next_event(ida_dbg.WFNE_SUSP, wait_timeout)

    try:
        new_rax = ida_dbg.get_reg_val("rax")
    except Exception as e:
        raise RuntimeError("Failed to read RAX after stepping: %s" % e)

    return new_rax

fs = {}
for i in range(1, 26):
    for c in range(ord('0'), ord('9') + 1):
        x = (i << 8) + c
        fs[hex(x)] = hex(set_regs_step_over(0x140081760, x, 0x14003198A))

import json
with open("C:\\...\\8_-_FlareAuthenticator\\precomputed.json", "w") as f:
    json.dump(fs, f)

# {
#    "0x01": "0x279342f",
#    "0x02": "0xc678db8",
#    "0x03": "0x87d0f40",
#    "0x04": "0xcc48d40",
#    "0x05": "0xc60a7f3",
#    ...
#    "0x1937": "0x128a844",
#    "0x1938": "0x953ac3b",
#    "0x1939": "0x2ebffff"
# }

Finding the correct password

Now the problem has become purely mathematical. We need to find $x_0, x_1, \dots, x_{24} \in \{ 30_{16}, \dots, 39_{16} \}$ , such that

\sum_{i=0}^{24} F[i] * F[(i \ll 8) + x_i] = \text{BC42D5779FEC401}_{16} = 847852483584640001.

While it may not be obvious what type of problem this exactly is, when we rewrite it in terms of $F$ being an unknown that can take one of some finite number of values based on $i$ and $x_i$ , it becomes clearer:

\sum_{i=0}^{24} F_{0,i} * F_{i, x_i} = 847852483584640001

In other words, we know $F_{0,i}$ and we are trying to find $F_{i, x_i}$ (by choosing an $x_i$ for every $i$ ) that solve the equation. This is known as a discrete domain linear equation, which can be solved by constraint programming solvers like Google's OR-Tools CP-SAT. Below is a vibe-coded snippet that does that.

from ortools.sat.python import cp_model

def solve_linear_discrete(Y, a, domains):
    """
    Solve Y = sum(a_i * x_i), with x_i in domains[i].
    Y: int
    a: list of coefficients [a1, a2, ...]
    domains: list of lists of possible integer values for each variable
    """
    model = cp_model.CpModel()
    x_vars = []

    for i, dom in enumerate(domains):
        x = model.NewIntVar(min(dom), max(dom), f"x_{i}")
        model.AddAllowedAssignments([x], [[v] for v in dom])
        x_vars.append(x)

    # Linear equation constraint
    model.Add(sum(a[i] * x_vars[i] for i in range(len(a))) == Y)

    # Solve
    solver = cp_model.CpSolver()
    solver.parameters.max_time_in_seconds = 10  # optional limit
    status = solver.Solve(model)

    if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
        return [solver.Value(x) for x in x_vars]
    else:
        return None

if __name__ == "__main__":
    with open("precomputed.json", "r") as f:
        precomputed = { int(k, 0): int(v, 0) for k, v in json.load(f).items() }

    def possibilities_for_idx(i, f):
        return [f[(i << 8) + c] for c in range(ord('0'), ord('9') + 1)]

    target_checksum = 0x0BC42D5779FEC401
    possibilities = { i: possibilities_for_idx(i, precomputed) for i in range(1, 25 + 1) }

    choices = solve_linear_discrete(
        target_checksum,
        [precomputed[i] for i in range(1, 26)],
        [possibilities[i] for i in range(1, 26)]
    )

    idxs = [possibilities[i + 1].index(x) for i, x in enumerate(choices)]
    print(idxs)

The above python script computes the solution to the equation in terms of $F$ and reconstructs the choice for each $x_i$ to give us the correct passcode, which it then prints to the output.

[4, 4, 9, 8, 2, 9, 1, 3, 1, 4, 8, 9, 1, 2, 1, 0, 5, 2, 1, 4, 4, 9, 2, 9, 6]

Entering this sequence into the authenticator gives us the flag:

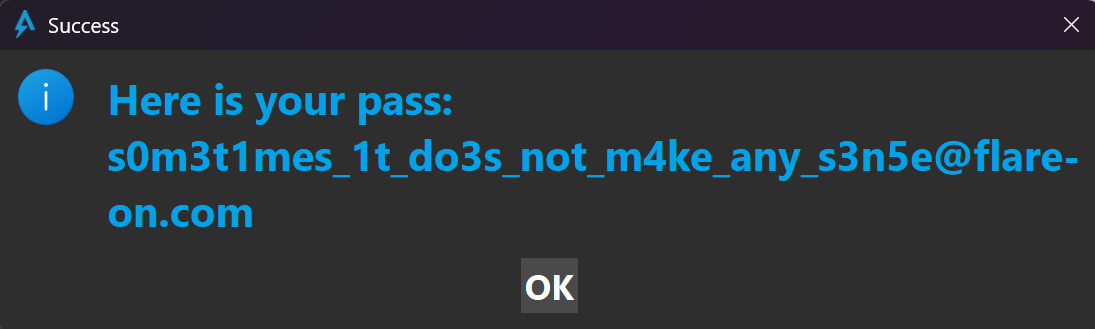
Flag

s0m3t1mes_1t_do3s_not_m4ke_any_s3n5e@flare-on.com